本节我们介绍一下差分隐私的概念,也是本公众号的核心工作所在,这一节,暂且用我认为读者可以理解的方式介绍一下什么是差分隐私。本文从以下几个方面展开介绍:
- 背景
- 去除标识化信息导致的隐私问题
- 背景知识攻击案例
- 我们需要什么样的隐私保护策略
- 差分隐私
- 一个简单的应用案例
- 待续
背景

在大数据背景下,如何保护个人信息安全以及防止隐私泄露一直是学术界和工业界的研究重点,从隐私保护角度来看,一般我们可能采取以下几种手段:
- 密码学手段(Cryptography):信息完全保真,但是计算复杂度太高。
- 匿名化手段(Anonymization):隐私保护水平比较低,可能会碰到NP难问题。
- 替代方法(Perturbation):暂不了解。
在这几种手段中,K匿名便是一种广为人知的隐私保护手段。现实生活中,我们通常以为去除了标识化信息,就可以保证个人的隐私保护,而新的研究逐渐表明,这种隐私保护的方法太过脆弱了。
去除标识化信息导致的隐私问题
当前的研究广为接受的一点是:当我们讨论安全技术,比如加密的时候,加密机制是假定公开的。一方面这有助于我们分析加密机制的复杂度;另一方面,很多情况下隐藏的敌手(Adversary)是知道加密实施的细节的。否则:你大可公开说,我发明了一种非常安全的加密机制,因为加密机制只有我知道。这可是一件会被嘲笑的事情。
与此同时,讨论隐私保护的时候也是一样。你永远不知道攻击你的人含有你哪些信息。对此,有些人可能嗤之以鼻:
Netflix曾经办了一个机器学习的比赛,旨在提高其推荐系统的准确性。为了保护公布的数据集中可能透露出的隐私问题,Netflix官方去除了数据集中的关键ID信息,然而,数据及发布没多久,研究人员便结合网上现有的知识和官方公布的数据还原出了数据集中的标识化信息。感兴趣的小伙伴可以参考这篇文章:Robust De-anonymization of Large Sparse Datasets。
对此,作者表示:“ Releasing the data and just removing the names does nothing for privacy. If you know their name and a few records, then you can identify that person in the other (private) database. ”
通过Netflix的案例,想必我们已经知道:直观上感觉安全的机制其实在精心设计的攻击面前毫无抵抗力。
背景知识攻击案例
| patient | has cancer |
|---|---|
| Amy | 0 |
| Tom | 1 |
| Jack | 1 |
我们不妨假定拥有一个和是否患有癌症有关的表,是否患有癌症对个人来说自然是相当敏感的问题,也需要我们保护。那么,假定敌手知道表中Jack在最后一行的话会发生什么呢?
如果此表支持查询患有癌症的人数,那么敌手自然可以进行以下两个查询:
- 前两行有多少人患有癌症
- 前三行有多少人患有癌症
利用两个回复的差,敌手就完全可以知道Jack是患有癌症的。所以从这个角度来说,是否能保护好个人隐私和敌手拥有的背景知识有关。敌手拥有的背景知识越多,被攻击的可能性就越高。
设想
背景知识就像薛定谔的猫,你永远不知道敌手有没有,也不知道他有多少。不妨?假定敌手拥有所有的背景知识?
当然不行,已有的数据敌手都知道了,那就没东西可以保护了。所以,我们就假定敌手拥有除了当前我拥有的数据之外的所有其他知识。
如果这种情况敌手还不能从我的数据中获取有关个人的知识,那不是爽歪歪?
差分隐私
在这个假定之下,如何从直观上设计出保护隐私的算法呢?
这时候我们需要重新回到“什么是隐私”这个话题上,学术界目前还没有对隐私有一个共识的定义,直观来说,如果从数据中获取到关于你的信息越多,我们倾向于认为你所受到的隐私侵犯越大。
那么,如果我对数据的查询完全得不到你的信息,是不是意味着完全没有泄露你的隐私(这个“你”就是我们要保护的对象)?当然是的,不过代价是,都得不到你的信息,那么你的信息也就没用,这当然也不是我们所希望的。我们希望的是在保证数据可用的前提下,尽可能少地泄露隐私。
因此,我们希望我们对数据的查询“几乎”得不到你的信息。也就是说,你在这个数据库中和你不在这个数据库中两种情况下我对数据库的查询得到的结果“几乎”一样,我们就更倾向于你的隐私得到了保护。也就是说我们希望:
既然在数据库中和不在数据库中结果都一样了,那肯定就意味着数据可用性为0了。所以“几乎”二字很重要,“几乎”的程度也就表示着隐私保护的力度。

为此,科学家们提出了“相邻数据集”的概念:如果两个数据集只相差一条记录,那么这两个数据集是“相邻数据集”。在这基础上,如果对于相邻数据集的查询结果相近,那么那相差的一条记录的隐私就得到了保护。
接下来很自然而言的一个问题,就是得到了多大程度的保护?还记得前面提到的“几乎”的概念吗?直观上,我们有:
在这个背景之下,Cynthia Dwork在2006年提出了差分隐私(Differential Privacy, DP)的概念。
Differential Privacy: A randomized algoritnm $\mathcal{M}$ with domain $\mathbb{N}^{|\mathcal{X}|}$ is $(\epsilon, \delta)-$differentially private if for all $\mathcal{S}\subseteq$ Range $(\mathcal{M})$ and for all $x,y\in\mathbb{N}^{|\mathcal{X}|}$ such that $||x-y||_1 \le 1$:
对这个定义可以这么理解:如果对于任何一个可能查询结果,机制M对于任何相邻数据集的查询结果都不可区分,那么就说机制M是满足差分隐私机制的。epsilon称为隐私预算(budget)。通常而言,budget越小,隐私保护程度越高,数据可用性越差。(这里的delta可以忽略不看)
这个定义中有两点需要体会:
- (x,y)是无序的,我们用概率比值来衡量相似程度
- 相邻数据集意味着对每一条记录都提供保护
根据这个定义,研究者就可以对数据集进行分析而保证任何一个数据集中的个体的隐私都不会被泄露。那么如何理解这个定义呢?首先需要知道什么是M以及为何M的输出是概率性的。
- 查询不应该是确定性的吗?为何会有概率?
在当前的很多隐私保护模型中,查询结果确实是确定性的。差分隐私机制引入的“随机化”就是通过将确定的输出以概率的方式呈现(可以理解为,以一定概率说假话)。

- 将确定性的结果概率化难道不会导致不精确吗?
这需要回到数据分析的目的来,即数据可用性。在大数据环境下,我们关心的是数据集中数据呈现出来的性质,规律等,而非单一个体的性状。要保障个人的隐私,必然会导致数据分析中引入误差。我们希望控制误差,差分隐私实际上也正式隐私保护程度和数据可用性之间的权衡。即如果下图中的两条曲线越近,隐私保护程度就越高。
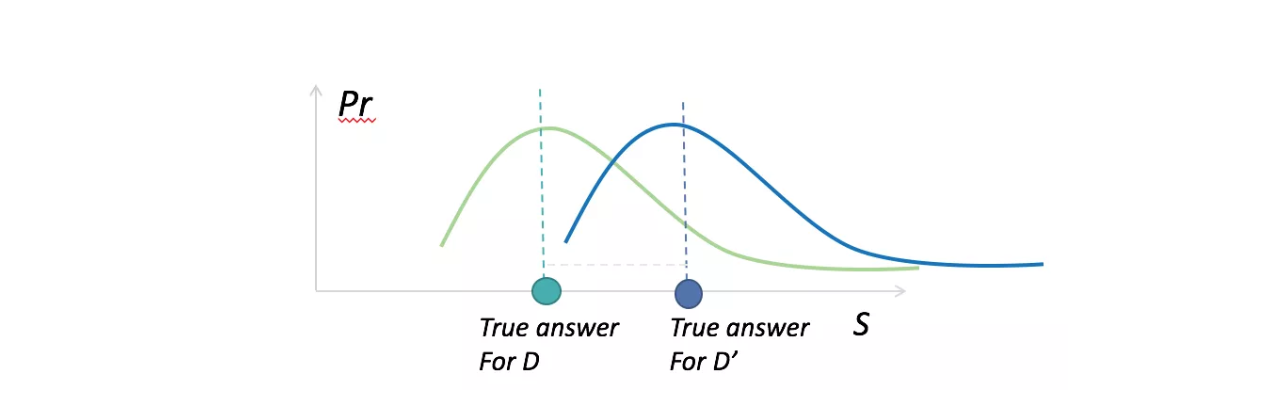
应用
DP只是一个定义,最初的DP甚至只是一种对隐私保护的一种至高目标,如何设计出满足DP机制的随机化算法M才是研究人员最关心的问题。本篇内容先不给出如何设计机制M,仅给出一个案例:
案例研究:如何通过抽样统计人群中抽烟人数的比例?
对于被调查者,是不希望直接回答自己抽烟与否的,因为在一定程度上,抽烟是一种和个人隐私紧密相关的问题。
只需要通过一枚硬币,就可以以差分隐私的方式解决这个问题。这个方法叫做Coin Flipping:
(1)扔一枚硬币,如果正面朝上,老实回答自己是否抽烟
(2)如果反面朝上,则重复扔一枚硬币,如果正面朝上就回答“抽烟”,反面朝上就回答“不抽烟”。
数据有效性(Utility)
首先,我们来看这个机制是否可以解决问题,我们用$P_a$表示被调查者抽烟的概率(即我们想获得的结果),用$P_b$表示我们收集到的抽烟人数的比例,则根据上面的过程有:
因此:$P_a = 2P_b-0.5$
所以根据统计的$P_b$可以估计出$P_a$,这个估计人群吸烟比例的方法是正确的(假设有足够多的样本)。
隐私性(Privacy)
数据有效性是对数据整体而言的特性,而隐私就更涉及到和个人有关。理想情况下,最好的隐私保护策略就是随机回答,但是随机回答会导致数据完全没有真实性。我们看一下CoinFlipping的过程,首先有:
S=[‘抽烟’, ‘不抽烟’]
因此我们可以计算出
P[‘抽烟’ | ‘抽烟’] = 0.75
P[‘抽烟’ | ‘不抽烟’] = 0.25
P[‘不抽烟’ | ‘不抽烟’] = 0.75
P[‘不抽烟’ | ‘抽烟’] = 0.25
那么我们自然而然就计算出了$\epsilon=\ln 3$,所以我们说 Coin Flipping 机制是提供了$\ln 3$-DP的。
直观感觉上来说,Coin Flipping是比较能保护隐私的,因为即使某人回答抽烟,我们只能得到他很可能抽烟(保证数据有效性),而无法确定此人是否抽烟(隐私性)。
待续
上面提到的一个应用仅仅针对二值回答才有效,如何对一般性的查询设计出一个满足差分隐私的随机化查询机制M呢?在DP的定义一出来之后,不就便广受研究人员的关心。
文中的部分配图来源于朱天清老师的课件,朱老师在学术上做了大量和差分隐私有关的工作,辛苦朱老师的付出。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


