在一章节《DP-Differential privacy概念介绍》中，我们介绍了什么是差分隐私以及通过一个简单的例子展示了差分隐私的应用案例。我们不禁想知道，有没有一个通用的满足差分隐私机制的针对数据库的查询算法的？

Laplace分布
Laplace噪声与DP
Laplace机制与应用
总结

Laplace 分布

Laplace分布是统计学中的概念，是一种连续的概率分布。如果随机变量的概率密度函数分布为：

$f(x|\mu,b)=\frac{1}{2b}\exp (-\frac{|x-\mu|}{b})=\frac{1}{2b}\begin{cases} \exp(- \frac{\mu-x}{b}) & x < \mu \\ \exp(- \frac{x-\mu}{b}) & x \ge \mu \end{cases}$

那么它就是拉普拉斯分布。其中，$\mu$ 是位置参数，$b>0$ 是尺度参数。画出来就是长这样：

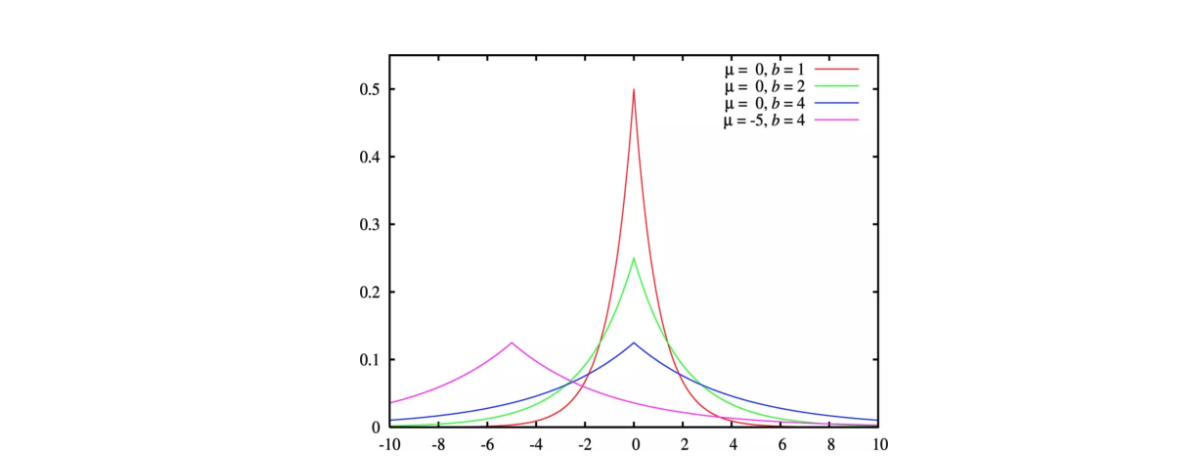
fig-laplace_curve

我们之前提到过，保护数据隐私的方法就是将原有的单一查询结果概率化。Laplace噪声就给我们提供了一个很好的概率化的方法。举个简单的例子，假如查询为“查询数据集中年龄小于20的人数”，并且查询结果为“50”：在传统模式下，输出就是50；在差分隐私模式下，会以比较大概率输出50左右的结果，也会以比较小的概率输出和50差别比较大的结果。但是，我们需要保证输出的期望为50（保证数据有效性）。

那么这个概率怎么用Laplace分布来呢？我们可以直接在输出结果50上加均值为0的噪声。直观上来说，我们通过Laplace将查询结果概率化了。那么是否Laplace噪声就满足差分隐私了呢？我们慢慢道来。

Laplace 噪声与DP

如何利用Laplace噪声产生符合DP的机制就成了我们主要研究的问题。我们依然想一下DP的设计目标：“有你和没有你查询结果相差不大”。那么现在问题就来了，这个“有你”和“没有你”在真实情况下相差多少呢？

研究这个问题是因为我们不限定用户对数据集做出什么样的查询，直观上来说，如果查询的是人数，那么“有你”和“没有你”相差不大（只会相差1），只需要加一个小一点的噪声即可造成两个结果的混淆；那如果我们查询的是人的工资呢，加一个很小的噪声显然是无法满足应用需求的（因为数据相差太大，稍微对数据的改变依然可以看出数据差别很大）。由此可见，如何设计DP机制是和查询紧密相关的。所以我们需要对查询有一个简单的了解：

也因此，科学家们提出了“敏感度”的概念，我们先来看一下定义（$f$ 就是我们的查询）：

$L_1$-sensitivity The $L_1$-sensitivity of a function $f:\mathbb{N}^{|\mathcal{X}|}\rightarrow\mathbb{R}^k$ is:
$\triangle f = \max \limits_{x,y\in\mathbb{N}^{|\mathcal{X}|}, ||x-y||_1=1} ||f(x)-f(y)||_1$

由于数据集中少一条记录就会对数据查询f的结果结果造成一定的影响，我们自然想知道，这个影响最大是多少呢？也就是上述定义中给出的敏感度的值 $\triangle f$ 了。

有了 $\triangle f$ 之后，我们自然想：$\triangle f$越大，噪声应该越大，$\triangle f$ 越小，噪声应该越小。这就给我们设计接下来的机制给了一定的启发。

The Laplace Mechanism: Given any function $f:\mathbb{N}^{|\mathcal{X}|}\rightarrow\mathbb{R}^k$, the Laplace mechanism is defined as:
$\mathcal{M}_L(x, f(\cdot),\epsilon) = f(x) + (Y_1, Y_2, ..., Y_k)$
where $Y_i$ are i.i.d. random variables drawn from $Lap(\triangle f / \epsilon)$

这里的$Lap(\triangle f / \epsilon) $即表示我们上面提到的拉普拉斯噪声中$\mu=0, b = \triangle f / \epsilon$. 同时上面的$k$表示的实际上是查询的维度。$\epsilon$是人为定义的参数，是DP中的隐私保护程度。

接下来我们将说明，上面这个简单的Laplace机制就满足$\epsilon$-DP。证明过程如下（如果有不理解的地方，欢迎和我私聊）：

假设$p_x$表示$\mathcal{M}_L(x,f,\epsilon)$的pdf（probability density function），$p_y$表示$\mathcal{M}_L(y,f,\epsilon)$的，则对于某个输出$z$，我们有：
$\begin{align} \frac{p_x(z)}{p_y(z)} &= \prod_{i=1}^{k} \frac{\exp(-\frac{\epsilon |f(x)_i-z_i|}{\triangle f})}{\exp(-\frac{\epsilon |f(y)_i-z_i|}{\triangle f})}\\ &= \prod_{i=1}^{k} \exp{\frac{\epsilon(|f(y)_i-z_i|-|f(x)_i-z_i|)}{\triangle f}}\\ &\le \prod_{i=1}^{k}\exp(\frac{\epsilon(|f(x)_i-f(y)_i|)}{\triangle f})\\ &=\exp(\frac{\epsilon \cdot ||f(x)-f(y)||_1}{\triangle f})\\ &\le \exp(\epsilon) \end{align}$

Laplace 机制及其应用

案例一：Counting Queries（统计查询）

一般来说统计查询形如这样：”How many elements in the dataset satisfy property P”。即查询数据集中有多少条记录满足给定的条件。根据敏感度的定义，Counting Queries 中敏感度为1。所以直接在查询结果上加 $Lap(1/\epsilon)$ 的噪声即可。

案例二：Histogram Queries（直方图查询）

在直方图查询中，首先作出数据的直方图，每一个直方图中的数据表示当前块（cell）中有多少记录。直方图查询即查询每一个cell中有多少记录。由于每个cell是独立的，改变数据集中一条记录只会影响到一个cell，因此敏感度为1。在这个模式下，和 Counting Queries 一样，只需要加上 $Lap(1/\epsilon)$ 的噪声。

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》