指数机制与Laplace机制

在Laplace机制中，我们首先对数据库进行查询，然后再查询结果之上添加一定的噪声使其满足DP的要求。因此，返回的数据通常只是“接近准确”的。那么差分隐私能否允许我们得到真实的结果呢？在这种情况下，指数机制应运而生。

指数机制（The exponential mechanism）是为我们希望选择“最佳”响应的情况而设计的，但直接在计算数量上添加噪声可以完全破坏其价值。例如在拍卖中设定价格，其目标是最大化收益，以及在最优价格上添加少量正噪声（为了保护投标的隐私）可以大大减少由此产生的收入。

为了理解接下来我们举个例子：

假设我们有大量的南瓜和四个投标人：A，B，C，D，其中A，B，C各自出价1.00美元，D出价3.01美元。如何制定最优出售价格？假如以 3.01美元出售，则收入为3.01美元（只有D买）；以1.00美元出售，收入为3.00美元（ABC购买）；以3.02美元出售，收入为零！

在这个案例中，每个用户的投标价格是涉及个人隐私的，而对于价格来说，我们自然不希望是加噪声了的。毕竟谁也不希望本来可以3美元出手的南瓜最后只卖了2美元。

如何实现指数机制

指数机制适用于回答具有任意实用程序（和任意非数字范围），同时保留差异隐私。给定一些任意范围 $\mathcal{R}$，首先我们需要定义一个实用性函数 $u$ ：

$u: \mathbb{N}^{|\mathcal{X}|} \times \mathcal{R} \rightarrow \mathbb{R}$

简单来说，这里 $\mu$ 的作用就是给用户拥有的数据打个分，分越高，表示这个数据越重要（比如上述案例中的价格，可以直接作为 $u$ 看待）。因此对于数据集 $X$，我们希望选取的元素有最大效益。

和 Laplace 机制一样，我们需要知道 $u$ 最多改变多少，所以我们定义：

$\triangle u = \max \limits_{r \in \mathcal{R}, ||x-y||_1 \le 1} |u(x,r)-u(y,r)|$

设计指数机制的出发点即为对于任意的 $r$ ，按照 $\exp(\epsilon u(x,r)/\triangle \mu)$ 的概率选取最优解即可满足差分隐私要求，因为：

$\ln \frac{\exp(\epsilon \cdot u(x,r)/\triangle u)}{\exp (\epsilon \cdot u(y,r) / \triangle \mu)} = \epsilon [u(x,r)-u(y,r)]/\triangle u \le \epsilon$

所以就有了我们的指数机制了：

The Exponential Mechanism: The exponential mechanism $\mathcal{M}_E(x,u,\mathcal{R}) $ selects and outputs an element $r\in \mathcal{R}$ with probability proportional to $\exp(\frac{\epsilon\cdot u(x,r)}{2\triangle u})$

翻译过来就是：设随机化算法 $M$ 输入为数据集 $X$ ，输出为一个实体对象 $r\in\mathcal{R}$, $u(X,\mathcal{R})$ 为可用性函数，$\triangle u$ 为函数 $u(x,\mathcal{R})$ 的敏感度，若以正比于 $\exp(\frac{\epsilon\cdot u(x,r)}{2\triangle u})$ 的概率从输入中选择并输出 $r$，则算法 $M$ 是 $\epsilon$-DP的。

应用案例

假设某基地正在举办一场体育比赛，可以选择的项目有{足球，排球，篮球，网球}四个项目，参与者们对这些项目进行投票，现在要确定一个项目是的整个决策过程满足$\epsilon$-DP，以每个选项的得票数量作为可用性函数，在给定隐私预算情况下，可以计算选择各个项目的输出概率：

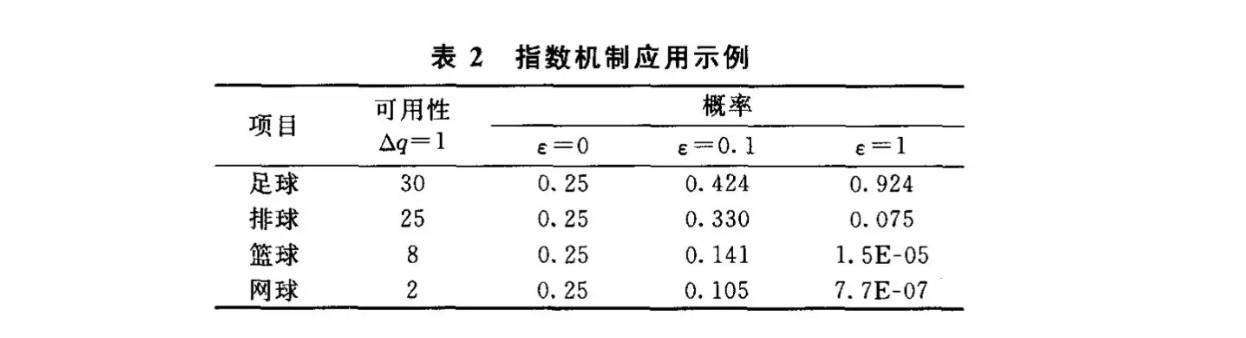
fig-table

上述案例中，当 $\epsilon = 0$ 时，提供完全的隐私保护但数据可用性为0，随着 $\epsilon$ 越大，选择出期望结果的可能性也越大。

指数机制的理论证明

此部分涉及指数机制的理论证明，不感兴趣的可以直接跳过。

$\begin{align} \frac{\Pr[\mathcal{M}_E(x,u,\mathcal{R})=r]}{\Pr[\mathcal{M}_E(y,u,\mathcal{R})=r]} &= \frac{(\frac{\exp(\frac{\epsilon u(x,r)}{2\triangle u})}{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(x,r')}{2\triangle u})})}{(\frac{\exp(\frac{\epsilon u(y,r)}{2\triangle u})}{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(y,r')}{2\triangle u})})}\\ &=(\frac{\exp(\frac{\epsilon u(x,r)}{2\triangle u})}{\exp(\frac{\epsilon u(y,r)}{2\triangle u})}) \cdot (\frac{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(y,r')}{2\triangle u})}{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(x,r')}{2\triangle u})})\\ &=\exp(\frac{\epsilon(u(x,r')-u(y,r'))}{2\triangle u}) \cdot (\frac{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(y,r')}{2\triangle u})}{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(x,r')}{2\triangle u})})\\ &\le \exp(\frac{\epsilon}{2})\cdot\exp(\frac{\epsilon}{2})\cdot(\frac{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(x,r')}{2\triangle u})}{\sum_{r'\in\mathcal{R}}\exp(\frac{\epsilon u(x,r')}{2\triangle u})})\\ &=\exp(\epsilon) \end{align}$

总结

本章介绍了 Laplace 机制及其证明和应用，下面是我的公众号二维码，所有的内容也同步在公众号上面，希望大家关注。