文章地址：https://ieeexplore.ieee.org/document/6517175
作者：Noman Mohammed; Dima Alhadidi; Benjamin C.M. Fung; Mourad Debbabi
发表会议：IEEE Transactions on Dependable and Secure Computing(2014)
目前被引用次数：56(2019.01.07)

本文讲了一种在两个实体下安全发布一个数据集的方法，并且发布数据集的过程是满足差分隐私的。下面是本文的笔记，序号和论文中的序号一样，有些地方我觉得对这篇文章的理解不重要，我跳过了，建议先看一下原文再来看我的笔记。

1 Introduction
2 Related Work
3 Privacy Model
4 Security Model
5 Two-Party Protocol For Exponential Mechanism
6 Two-Party Differentially Private Data Release Algorithm
7 Performance Analysis
8 Discussion（略）
9 Conclusion（略）
10 思考

1 Introduction

在现实生活中，很多时候是需要联合多个厂商对同一类型地数据进行处理的。我们据这样一个例子，银行A和贷款公司B，他们都有着某些人的一些数据记录（理想化，我们假定这些人既出现在A的数据集中也出现在B的数据集中，而且有着同样的ID，比如身份证号码）。那么数据集A和B中的信息可能是这样的：

A: (ID, Job, Balance)
B: (ID, Sex, Salary)

这时候A和B就想把自己的信息综合起来，这样可以提供更好的决策服务，同时，他们也希望这个数据可以给他们的合作公司，比如信用卡公司C。所以这个应用环境中就存在着信息共享和数据发布两个过程。当然，我们知道，隐私是一个很重要的考虑点，如何在保护隐私的前提下进行数据共享和发布呢？

为了更形象化地说明这个问题，我们举一个案例：

Example.1 拥有着A拥有数据表D_A(ID, Job, …, Class)，拥有着B拥有数据表D_B(ID, Sex, Salary, …, Class)，如下表所示。在这些数据中ID和类标class是共享的。对于总的数据来说，这两个子数据集就是 Vertically Partitioned 的。

fig01

在信息集成的过程中，我们很显然发现可以通过联合ID的方式来进行将两个数据集合并，但是已有研究表明，这是可能受到 linking attack 攻击的。

那这篇文章就是研究如何做这么个事情了，要集成数据同时要发布数据。文章主要有以下几个贡献点：

提出了可以用于 two-party 的指数机制
首次提出了对于垂直分割数据的满足差分隐私的数据发布方法，并且这个方法是满足安全多方计算的。
通过实验表明，发布的数据在数据挖掘任务中是很有用的

Related Work 部分主要列举了当前的一些研究进展，我就不提了，在这里提几个和背景有关的知识。

数据交互方法

在现有的应用系统中，一般分为两种交互模式：Interactive 和 Noninteractive，即交互式和非交互式。交互式框架下，用于提交一个请求，然后别人对这个请求作出回应，用户是拿不到原始数据的。在非交互式框架下，用户可以拿到一个发布的数据，至于用于对这个数据做什么，数据源无法控制，毕竟数据已经在用户手里。因此，出于对安全的考虑，发布的数据往往是含噪声的。非交互式方法可以搜索一下Privacy-preserving Data Publishing.

实体个数

我们也关心数据是不是被多个实体所拥有，在单一实体下，此实体拥有所有数据。在多个实体的情况下，不同实体拥有不同类型的数据，这些数据有可能是 Horizontally Partitioned，也可能是 Vertically Partitioned 的。在多实体情况下，我们当然希望可以集成所有的数据来进行数据分析。

Partition

数据分割方法一般分为水平分割和垂直分割，即通常提到的Horizontally Partitioned Data 和 Vertically Partitioned Data。最简单理解就是水平分割不同用户拥有不同行，垂直分割不同用户拥有不同列。看下面两个图就很容易懂了。

水平分割，即我们常说的按行分割。

fig-partition01

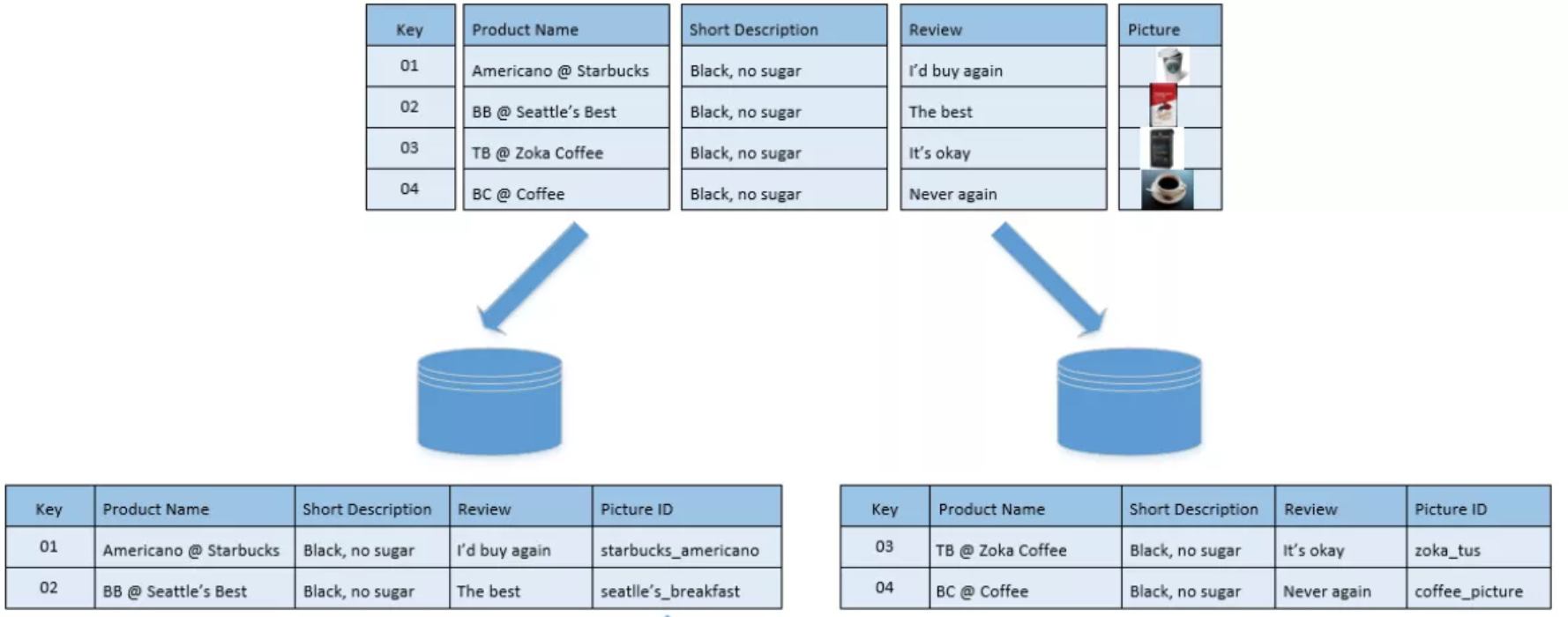
垂直分割，即我们常说的按列分割。

3 Privacy Model

本文使用的隐私模型为差分隐私，差分隐私的概念在本网站其他页面已经阐述过，在此就直接给出论文中使用的定义：

$\epsilon$-differential privacy: A randomized algorithm Ag is differentially private if for all data sets $D$ and $D’$, where their symmetric difference contains at most one record (i.e., $|D-D’|\le1$), and for all possible anonymized data sets $\hat{D}$:
$\Pr[Ag(D)=\hat{D}] \le e^\epsilon \times \Pr[Ag(D')=\hat{D}]$
where the probabilities are over the randomness of $Ag$.

在本论文中这个机制Ag的输出是一个数据集，我觉得这么定义是没问题的，但是后面又说了实现差分隐私的方式是在输出上面加一个Laplace噪声，就有点前后矛盾，因为在数据集上加噪声这个操作目前是没有的。

4 Security Model

这里有两个知识点需要注意，可以不需要知道细节，但是需要知道这么个工具。分别是Random Value Protocol (RVP)和 Secure Scalar Product Protocol (SSPP)。分别是干什么的呢：

RVP: RVP机制允许两个实体共同产生一个随机变量。

SSPP: SSPP可以安全地计算两个向量的数量积。

这两个机制来源于两篇论文，以后有时间的话可能会更新这两个机制的介绍，我也挺感兴趣的。

5 Two-Party Protocol For Exponential Mechanism

这个章节讲了如何在 two-party 之间进行指数机制。在了解两个实体间的指数机制之前，我们有必要了解一下什么是指数机制，可以参考本网站关于指数机制的描述。

在讲解 two-party 的指数机制之前，我们重新回顾一下指数机制的另一种实现手段，假设有三个数据分别为：

（篮球，8）
（足球，2）
（网球，1）

我们假设 ε = 1，那么对应篮球、足球、网球权重分别为$e^4$, $e$, 和 $e^{0.5}$次方。

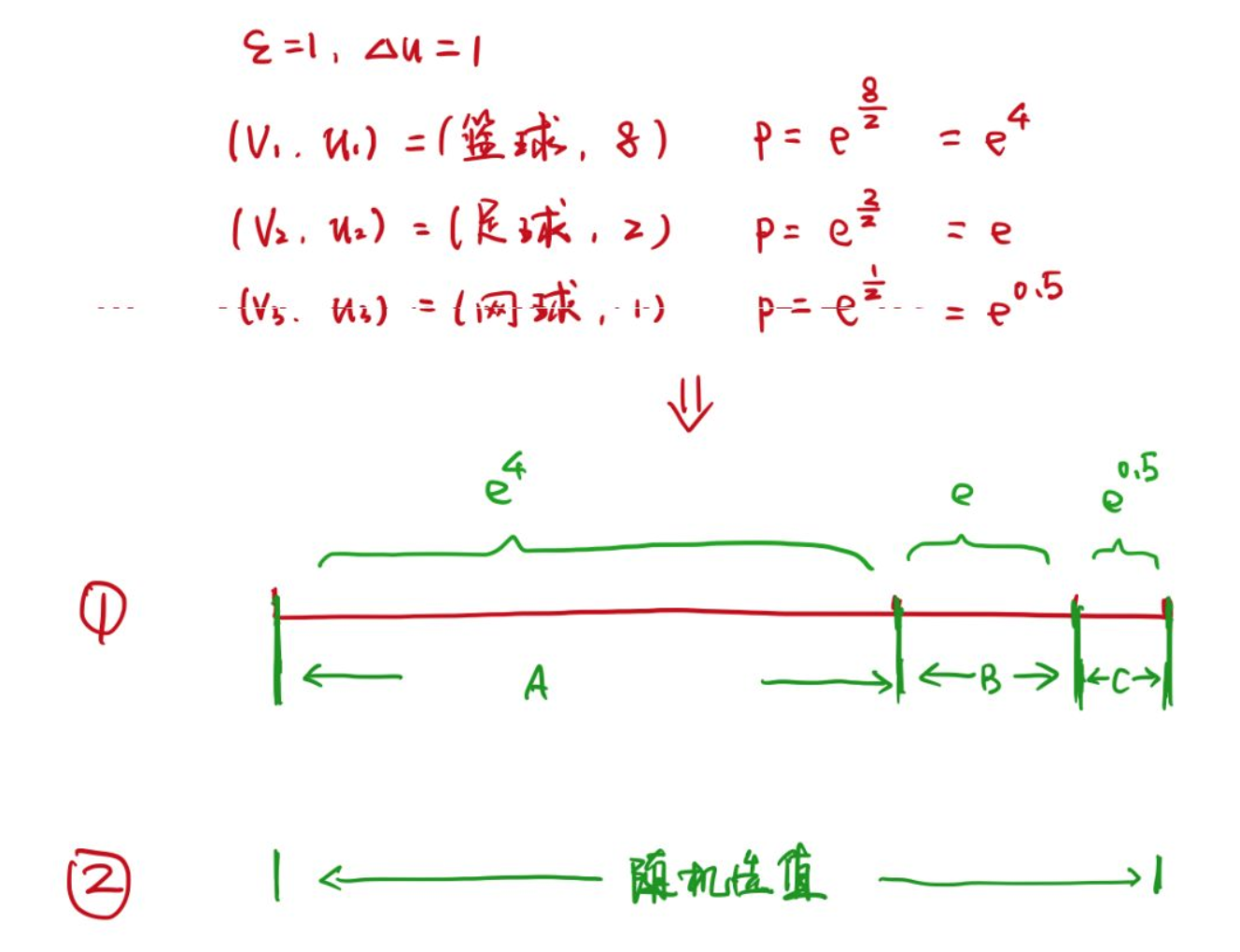
fig-myexample

所以我们先计算出 $a = e^4+e+e^{0.5}$，然后在 $[0,a]$ 之间任意选取一个随机数，如上图的ABC三个区间，落到A则选择篮球，以此类推。这样，我们就通过产生随机数的方式模拟了指数机制的产生过程。明白了这个过程，对于two-party的过程也就没有那么难理解了。

首先我们看一下程序的输入是哪些：

Finite discrete alternatives $<(v_1, u_1), …, (v_n, u_n)>$, where a pair $(v_i, u_i)$ is composed of the candidata $v_i$ and its score $u_i$. Parties $P_1$ and $P_2$ own $(v_1, u_1), …, (v_j, u_j)$ and (v_{j+1}, u_{j+1}),…,(v_n,u_n)$ respectively.
Privacy budget $\epsilon$.

这个输入其实就是指数机制里面的输入，不过现在数据分布在两个实体而已。然后我们再来看再两个实体之间如何进行指数机制，算法如下：

fig03

这个算法实际上就是先算出S1+S2，然后再这个范围内通过双方产生R1和R2的方式产生随机数R=S1+S2，然后L1+L2用来表示当前选择的那一个区间，如果选择的区间就是S1+S2那么就说明对应的值是指数机制的输出。COMPARISON 函数返回 0 如果 R1+R2 = L1+L2。

看到这里，相信对于这个算法的机制已经有了大致的了解。首先，这个机制很显然是符合指数机制的，也就是说，算法1是DP的。当然，其实我们还有一个假定，就是参与指数机制的实体都是 semi-honest 的，也就是说我们实际有一个 semi-honest adversary model 是作为背景的。也正因为如此，这个算法也是安全的。

实际上到这里为止，这个算法在实现的过程中还是会存在问题的，因为在计算的过程中存在精度的问题。所以作者取了一个巧，就是我们假定所以计算的结果进行一个 floor 操作，比如 $e^1 = 2.71828$，那么我们可以定一个$l$，用来表示小数点后面取多少位，例如：$l=1$ 就取27。这个$l$ 越大的话，有效数字就越多，就需要更多的存储空间了。

fig05

当然，算法复杂度也是一个需要分析的点，在这里我们就不阐述这个算法的复杂度了，可以参考原文。

6 Two-Party Differentially Private Data Release Algorithm

接下来就讲到本文的正题部分，如何在 Two-party 之间共享数据。我们还是以第一节中 Table1 的数据作为案例来如何集成两个表的数据。这里再放一次这个表：

fig01

首先，处于隐私性需求，我们需要一个叫 taxonomy tree，这个东西可以想象为用来控制信息细粒度，对应我们的表的话大概长这样:

fig02

通过这个 taxonomy tree，我们可以发现越顶层的数据含义越模糊，越底层的数据含义越精确。接下来我们就直接把算法放出来，然后再进行解释：

fig-mainalg

大致的分析过程可以先参考下图：

首先，我们先建立了只含有一条数据的总表，这条数据为（any_job, any_sex, [18,99)）即包含所有可能。同时，当前的分裂属性为：

Cut = {Any_job, Any_sex, [18,99)}

然后算法的4-18行是根据上一小节提到的 two-party 的指数机制来决策出一个需要分裂的属性，比如第一次可能决策树的属性为any_job，再根据 taxonomy tree，接下来的分裂属性就变成了

Cut = {Professional, Artist, Any_sex, [18,99)}

以此类推，这样就可以一直划分下去，直到划分h次，划分结束。

注意我们是需要发布数据集的，而划分的结果是没有计数字段的，所以我们还需要得到每个划分结果下的统计个数。

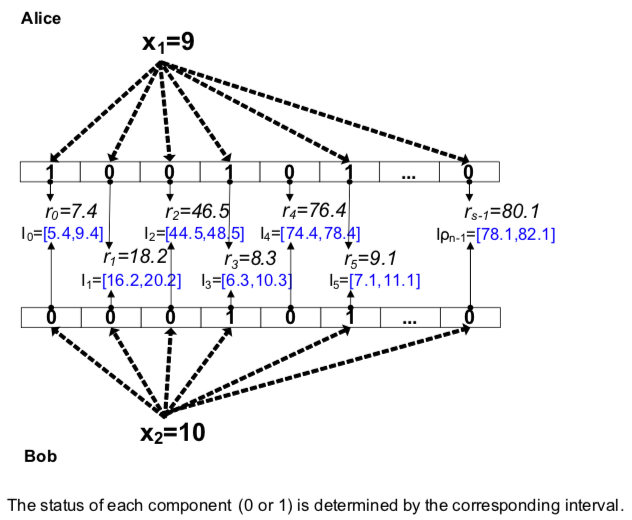
比如对于划分 {Professional, M, [18,99)}，我们怎么知道满足这种条件的一共有多少人呢？因为数据是被双方所共同拥有的，而双方又不能透露自己数据，这时候就需要用到之前提到的SSPP算法了。首先，两个实体在本地对自己数据进行统计，各得到一个向量：

fig07

这时候，Party A得到向量 [0000111011]，Paryt B得到向量[1110001010]，我们利用SSPP的性质，就可以在不泄露信息的前提下安全计算：

$\begin{align} Z_1 * Z_2 &= \sum_{i=1}^{10}(Z_1[i] \times Z_2[i]) \nonumber\\ &= 0 + 0 + 0 + 0 + 0 + 0 + 1 + 0 + 1 + 0 = 2 \nonumber\\ \end{align}$

所以我们就知道在集成的数据集中，满足{Professional, M, [18,99)}的有2人。

接下来，我们再进行加噪，得到一个含有噪声的数据。那么两个实体如何共同确定一个Laplace噪声呢？者需要用到这样一个性质：

Lemma 6.1 Let $Y_i \sim \mathcal{N}(0,\lambda)$ for $i\in \{1,2,3,4\}$ be four Gaussian random variables. Then the random variable $Lap(2\lambda^2)$ is equal to $Y_1^2+Y_2^2-Y_3^2-Y_4^2$.

这个引理就是说我们可以用四个高斯分布来模拟得到一个Laplace噪声，真的很神奇，所以算法3的22行实际上就是引理6.1的运用。

对于算法3的DP性质，论文中说是满足ε-DP的，因为有ε/2的噪声用于指数机制，ε/2的噪声用于Laplace机制。所以总的是ε-DP。实际上，我没有完全明白第3行 ε’ 的值的由来。

7 Performance Analysis

为了说明实验的有效性，实验设置了一定的基准：

Baseline accuracy (BA) is the classification accuracy measured on the raw data without anonymization;
BA-CA represents the cost in terms of classification quality for achieving a given 􏰓-differential privacy requirement;
Lower-bound accuracy (LA) is the accuracy on the raw data with all attributes (except for the Class attribute) removed—that is, all the predictor attri- butes for all the records are generalized to the topmost value;
CA-LA represents the benefit of our method over the naive nondisclosure approach.

讲完了基准，接下来就讲实验结果了。

fig08

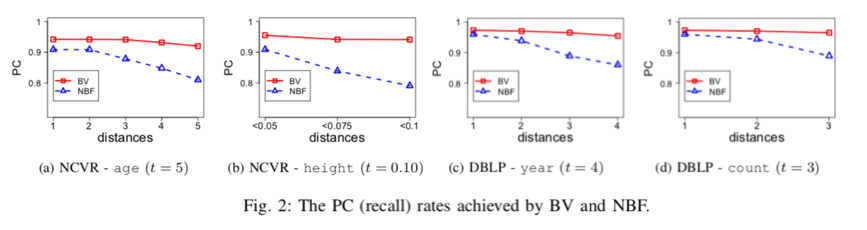
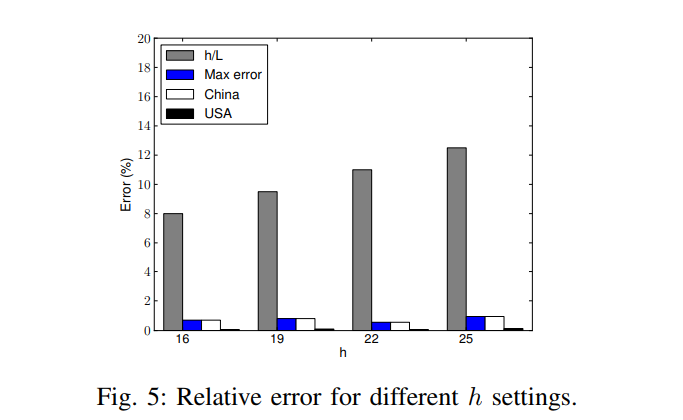
图3是在Adult数据集下的分类准确率，实验结果可以参考这个图，也没有什么好解释的。

图4也展示了精确度，这里有和其他方法的比较，DiffGen是其他论文中提出的方法，可见本文中的方法DistDiffGen和DiffGen相比总体来说还是有优势的。DAKA是基于K匿名的方法，由于其不是DP的所以DAKA的准确率是不变的。

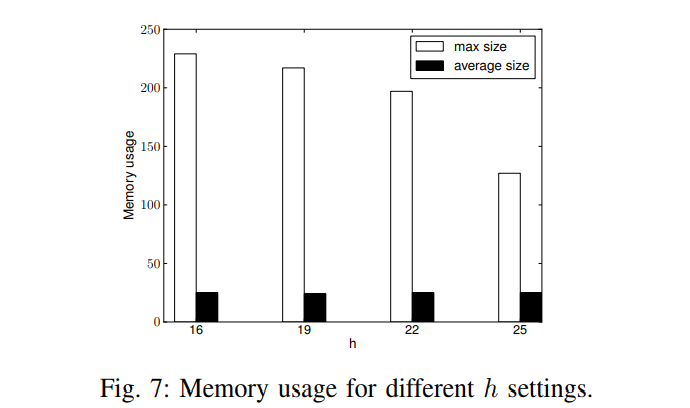
除此之外，文章还分析了效率问题，这里就不阐述了。

10 思考

文中最核心的算法Algorithm3设计的意图是为了产生一个ε-DP的机制，首先将ε/2的噪声用于指数机制，再将ε/2的噪声用来做count的计算。

那么，假如我们在做count计算的时候不加噪声，而是直接选用SSPP的结果，也就是说此时的算法Algorithm3就是ε/2-DP的，我们暂且把这个算法称为算法4。也就是说算法4比算法3的隐私保护程度更高。

但是，算法4的数据有效性是肯定比算法3的数据有效性要高的，毕竟在 count 计数的时候没有加上额外的噪声。

所以，为什么要进行对count加噪声这个过程呢？

实际上，在这个过程中，我赞同指数机制部分是 $\frac{\epsilon}{2}$-DP的，我也赞同count加噪声这个部分是$\frac{\epsilon}{2}$-DP的，但是我不认为将这两个机制直接组合的结果就是$\epsilon$-DP的。毕竟这两个过程作用的数据对象是不一样的。不是直接符合DP的组合机制。

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》