文章地址:https://dl.acm.org/citation.cfm?id=3271736
标题:Privacy Preserving triangle counting in large graphs
作者:Xiaofeng Ding; Xiaodong Zhang; Zhifeng Bao; Hai Jin.
发表会议:Proceedings of the 27th ACM International Conference on Information and Knowledge Management
Triangle counting是社交网络中挖掘关系的关键参数。然而,直接公布从三角形计数中获得的结果可能会带来潜在的隐私问题,这为隐私保护三角计数带来了巨大挑战和机遇。在本文中,我们选择使用差分隐私来保护大规模图形中的三角形计数。为了降低大图中引起的较大灵敏度,我们提出了一种新颖的图投影方法,可用于获得不同分布中灵敏度的上界。特别是,我们用两种直方图发布满足节点差分隐私的三角形计数:三角形计数分布和累积分布。此外,我们将隐私保护三角计数的研究扩展到局部聚类系数发布的应用之中。实验结果表明,累积分布可以更好地拟合实际统计信息,并且我们提出的机制在保持差分隐私要求的同时,实现了更高精度的triangle counting。
下面是本文的笔记,序号和论文中的序号一样,有些地方我觉得对这篇文章的理解不重要,我跳过了,建议先看一下原文再来看我的笔记。
- 1 Introduction
- 2 Related Work
- 3 Preliminaries and Problem Formulation
- 3.1 Differential Privacy
- 3.2 Privacy Preservation on Triangle Count
- 3.3 Utility Metrics
- 4 Our Algorithm
- 4.1 Edge-deletion Based Data Projection
- 4.2 Cumulative Histogram and Utility Metrics
- 5 Local Clustering Coefficient
- 6 Datasets and Experiments
- 7 Conclusions
- 8 个人反思
1 Introduction
本文介绍了一个叫做 Triangle counting 的问题,在图中,triangle count 还是一个比较有用的东西的,所谓 Triangle counting,实际上就是数三角形,我们来举个例子:
在这个网络图中,我们来看下P1,其对应的三角形有123,124和134,所以可以数到3个三角形,其对应的 triangle count 为3。所以节点对应的三角形个数分别为(P1, 3), (P2, 4), (P3, 4), (P4, 5), (P5, 1), (P6, 1), (P7, 0)。因此连接到0个三角形的节点有1个,连接到1个三角形的节点有2个,连接到3个三角形的节点有1个,连接到4个三角形的节点有2个,连接到5个三角形的节点有1个。所以我们就可以做出右边的分布图了。
而已有的研究表明,直接发布triangle count的直方图是存在隐私泄露问题的。作者在论文中给了一个例子:在上图中,假如敌手知道除了P4的人都在网络中,而不清楚P4是不是在网络之中,那么在他得到了这个直方图之后,和已有的信息比较,那么他就能知道P4在网络中而且还能知道P4连接到了哪些节点。(这个例子总觉得有点怪怪的)
在这篇论文中,作者研究的问题就是如何在保护隐私的情况下发布图的信息。
2 Related Work
这部分讲了当前对网络结构的 privacy protection,也提了其他论文里面处理方法。为什么要用差分隐私呢,当然是因为现有的模型理论上不能抵抗背景知识攻击。反正用差分隐私的论文里面大都会有这么一句话,当然这也没错。
因为论文的内容部分不涉及当前的工作,所以我也没有去看参考的文章,就不在这里阐述了。
3 Preliminaries and Problem Formulation
3.1 Differential Privacy
差分隐私的定义是本公众号提到的最多的东西了,这里也不再阐述,可以参考文章《DP-Differential Privacy概念介绍》。
同时需要注意一下差分隐私的 Laplace 实现中,需要知道全局敏感度,其定义在本文中有用到,因此再提及一下:
对于查询$f: D\rightarrow\mathbb{R}^{k}$ 来说,其全局敏感度为:
有了全局敏感度之后,添加噪声大小为$Lap(\triangle f/ \epsilon)$的拉普拉斯噪声即可实现差分隐私。
3.2 Privacy Preserving on Triangle Counting
问题定义:给定无标图 G=(V, E),我们需要发布每个节点的triangle count分布。可以被认为是这么一个回答:有多少连接着x个三角形的节点?其中,x就是可能的三角形个数。由于发布节点的triangle count是涉及用户隐私的,发布数据需要是保证privacy-preserving的并且希望发布的数据和原有数据具有类似的统计特性。
在一个网络图中,其实存在着这样一个问题,我们可以保护边,也可以保护节点。这篇文章采取了保护节点的思路,主要有以下两个出发点:
- 在社交网络之中,一个节点就代表着真实世界的一个用户。当我们谈论隐私保护的时候,我们更倾向于谈论用户的隐私保护
- 做节点的隐私保护比做边的隐私保护更具有挑战性,去除网络结构中的一条边带来的 triangle count 计数较小,而去掉一个节点会带来网络结构中较大的变化。
3.3 Utility Metrics
Utility Metrics 主要讲的是如何衡量发布的数据和原始数据的相似性,对于直方图来说,作者采用L1距离。本来想翻译一下的,但是想到中文不如英文简练,就直接采取了原文的表达。L1其定义如下:
$L_1$ Distance: Given two histograms $h$ and $h’$ in a V-dimensional vector space, the $L_1$ distance between them is:
Where $h$ and $h’$ are vectors of $h=(h_0, h_1, …, h_{V-1})$, $h’ = (h_0’,h_1’,…h_{V-1}’)$.
同时,对于发布的累积直方图,作者采用 KS-distance (two-sample Kolmogorov-Simirnov test) 来评估其有效性。KS距离定义如下:
KS Distance: Given two histograms $h$ and $h’$, the KS-distance between them is:
where $CDF_{h(i)}$ represents the value of cummulative distribution of $h_i$.
这两个定义如果比较陌生的话,我这里给一个简单的例子,重新考虑一下Introduction给出的网络结构图,为了方便,我再贴一遍:
在这个网络图中,节点对应的三角形个数分别为(P1, 3), (P2, 4), (P3, 4), (P4, 5), (P5, 1), (P6, 1), (P7, 0)。因此连接到0个三角形的节点有1个,连接到1个三角形的节点有2个,连接到3个三角形的节点有1个,连接到4个三角形的节点有2个,连接到5个三角形的节点有1个。
在累计直方图中,我们可以知道连接到不超过0个三角形的节点有1个,连接到不超过1个三角形的节点有三个。。。以此类推可以得到累计分布直方图。
如果现在去掉节点P5,那么现在的图就是这个样子:

这时候,节点对应的三角形个数分别为(P1, 3), (P2, 3), (P3, 4), (P4, 4), (P6, 1), (P7, 0)
因此,两个直方图分别是(1,2,0,1,2,1)和(1,1,0,2,2,0),根据L1距离的定义,其L1距离为:
KS距离需要计算分布,在此我就不给出了。
4 Our Algorithm
主体工作部分,作者干了这么一件事情:首先提出了自己的算法,然后给出了基于这个算法的直方图发布和累计直方图发布中全局敏感度的上界,当然,也要分析发布数据的Utility。
4.1 Edge-deletion Based Data Projection
试想,假如给你一个网络图,让你对图进行处理,使得所有节点的triangle count 都不大于给定的数,那么你会怎么处理呢?其实也不是很难想到,当然是删边嘛。在给出具体算法之前,作者给了一个 Stable sequence 的定义,和文章内容没有什么联系,所以可以跳过。作者接下来直接给出了删边的算法$T_\lambda$:

这个算法的思路比较暴力,就是遍历所有的节点,然后如果当前的节点 triangle count 大于给定阈值,就需要删掉某些边。那么删掉那些边呢?再给出的算法1中,如果发现当前节点 $v_i$ 需要删边,那么首先找到 $v_i$ 所有链接的节点,然后在链接的节点中找到度最大的节点 $v_j$,然后删掉边 $v_i\text{-}v_j$。
算法1的输入是原始网络结构图 $G$,输出是图 $G^{\lambda}$ 其满足所有的节点度数都不大于 λ。
构图需谨慎,删边有风险。我们知道,边也是不能随便删的,作者举了这么一个例子:
你看,如果把中间这条边删掉,那么所有的三角形都会消失。所以,其实就删边来说,其实也可以有很多策略的:
- DR策略:delete edges randomly.
- DL策略:delete edges from the linked nodes which have a larger degree.
- DS策略:delete edges from the linked nodes which have a smaller degree.
因此,我们现在就可以生成一个满足要求的图了。然后需要做的就是如何发布图的直方图,其算法$Tr^\lambda\text{-Hist}(G)$ 为:

作者利用Laplace机制,所以关键的就是如何确定噪声的大小。在这里,作者用了DP基于节点, 即希望对于图中的任意节点来说,这个节点存在与不存在对发布直方图的影响不大。作者给出的误差是根据引理4.2:
Lemma 4.2: Given any two graphs $G$ and $G’$ which differ by only one node, we have:
即经过算法1产生的图中,如果采用L1距离,一个节点的小时在统计图上的影响最大为 4λ+1。
可能是为了将问题说得更明白一些,作者的证明过程有点点小乱,我们重新理一下为什么是4λ+1。我们在这个图中假设要删掉节点1:

首先,对于当前节点来说,假设其 triangle count 为m,则意味着当前节点有着m个三角形。对于节点1来说有m=3,即会影响到三角形123,124,134。实际上,每删除掉一个三角形,就会删除掉两条边,即影响2个节点。对于每一个受影响的节点来说,其三角形统计数会减少1,而在直方图中,减小1的对应的统计个数就会增加1,所以带来的误差为2。经过这个分析过程,删除一个三角形在L1距离上的影响为4。另外我们还需要注意到,网络图中少了一个节点,所以总的影响程度为4m+1。根据算法1的性质,误差的上界就为4λ+1了。
4.2 Cumulative Histogram and Utility Metrics
同样,作者也给出了累计直方图发布的算法,累计直方图发布其实也比较简单,重要的是噪声的多少。其算法如下:

和前面一样,我们重点关心的是累计直方图中一个节点消失所带来的误差上界,作者由引理4.3给出:
Lemma 4.3: Given any two graphs $G$ and $G’$ differing only by one node, we have:
作者说在累计直方图发布中,删除一个节点所带来的误差上界为 2λ+1。为什么累计直方图发布和直方图发布的噪声大小不一样呢?
和前面的分析一样,假如当前节点由m个三角形,那么删除一个三角形会影响2个点,我们这两个点对应的triangle count都会减少1个
triangle count 小于等于 x 的节点数目是多少个,假如当前删除的点为A,并且B和A相连。那么删除A之后,需要删除AB连线,B的triangle count会减少1(由于图中有其他三角形影响关系,可能不止减少1,但是当前边只会影响1个计数)。我们假设B的 triangle count 个数为k,则在直方图发布下,k对应的个数会减少1,k-1对应的个数会增加1,所以一条边的影响为2。那么对于累计直方图就不一样了。在累计直方图下:
- triangle count 小于等于 k-1 的个数会增加1
- triangle count 小于等于 k 的个数不变
也就是说,删除m个三角形带来的变化只有2m,而不是像直方图发布中的4m。当然因为还需要删除当前节点,在当前节点计数中,也会带来1的变化量。此外,我们还需要注意,由于删除当前节点,查询 “triangle count no more than x(x>m)” 的结果都会少一个1。即从 m+1 到 λ 的计数都会少1,这部分影响了 λ-m+1,所以其敏感度为这两部分的和,一共是 λ-m+1 +2m = λ+m+1 <= 2λ+1。至此,引理4.3就证明出来了。
5 Local Clustering Coefficient
在讲解这部分的内容之前,我们需要提前了解一下聚合系数的概念,聚合系数的概念在wiki上可以找到对应的解释。
直观来说,聚合系数描述的是网络中“你是你朋友的朋友的可能性”,听上去比较绕口。不妨看一个简单的图:
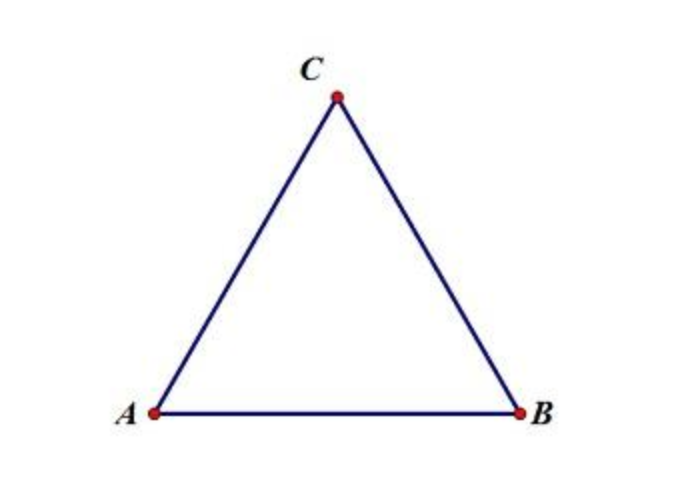
上图中,AB,AC,BC都相连,如果从A的角度来看,C是A朋友的朋友(因为C是B的朋友),另一方面,C是A的朋友,即A朋友的朋友(C)也是A的朋友。
所以我们是这样计算节点的聚合系数的,首先看节点有多少个相邻节点,假设为n,那么就存在 n(n-1)/2 种可能的情况有连接,再看这么多种情况里面有多少个是真实连接的。然后计算比例。

回到原有的图中,对于P4来说,有三个节点相连,两两组合可能有15中情况,在这15中情况里面有5个是真实相连的,所以其聚合系数为1/3。实际上,这5个真实相连就是 P4 的节点 triangle count 为5。
在作者论文中,算法4存在问题,因此我们讲解过程中略过。读者放心,这个算法不影响对后面的理解。
好了现在我们的目标就是需要发布聚合系数的直方图。因为聚合系数不像计数那样以1为单位,所以我们先对聚合系数进行区间然后再统计。比如我们分为两个区间,就是计算聚合系数在 [0,0.5) 和 [0.5,1] 的节点个数。
所以作者接下来的算法就是发布区间上聚合系数的节点个数。

算法的第1行是进行一个减边处理,限制每个节点的triangle count。然后2-3行计算每个节点的 local clustering 系数,4-9 行看起来比较高大上,实际上就是进行了一个分组然后统计聚合系数在对应分组的节点个数,作者的做法是给定一个 k,然后把区间 [0,1] 分成 k 个等大的区间,然后再进行统计。13行才是关键,和前面的分析一样,这里涉及到噪声的大小。
这里的噪声大小也是 4λ+1,其证明过程和Lemma 4.2是一样的,在此就不加过多说明了。
值得注意的是,如果发布累计直方图,噪声的大小并不是前面的 2λ+1,而是在引理5.4中给出:
Lemma 5.4: Given any two graphs $G$ and $G’$ differing only by one node and given the group number $k$, we have:
和前面的分析一样,假设要去掉的节点的 triangle count 为 m。每去掉一个triangle 就会影响到 2 条边,就会影响到 2m 个节点的聚合系数。而聚合系数的变化不像 triangle count 的变化一样每次只会减少 1,聚合系数的变化是跳动的,作者认为最差的情况就是从 1 变成 0,这会导致一个聚合系数的变化在 k-1 个分组上带来变化,所以带来的 L1 距离上的变化量是 2m(k-1),又由于这个点消失了,所以最多还会有 k 个分组变化,综合来看最后的 L1 距离就是 2m(k-1)+k。
当然,可以说作者考虑这个问题的时候,是放宽了考虑的,我认为这并不是严格的下界。我也仔细考虑了这个问题,除了想到一个没有考虑到的地方之外,我也并不能给出更精确的上界(至少目前发现这个结论并不是完全正确的)。
6 Datasets and Experiments
首先我们看一下作者用的数据集,作者采用了三个真实的数据,分别来源于:
- Wiki-Vote: the network from Wikipedia of who-votes-on-whom
- Cit-HepTh: Arxiv High Energy Physics paper citation network
这三个数据集的特点如下表所示:
| Dataset | #$V$ | #$E$ | $Tri_{sum}$ | $Tri_{max}$ | $Tri_{avg}$ |
|---|---|---|---|---|---|
| Wiki-Vote | 7115 | 103689 | 608389 | 30940 | 86 |
| Cit-HepTh | 27770 | 352807 | 1478735 | 33527 | 53 |
| 81306 | 1768149 | 13082506 | 96815 | 1698 |
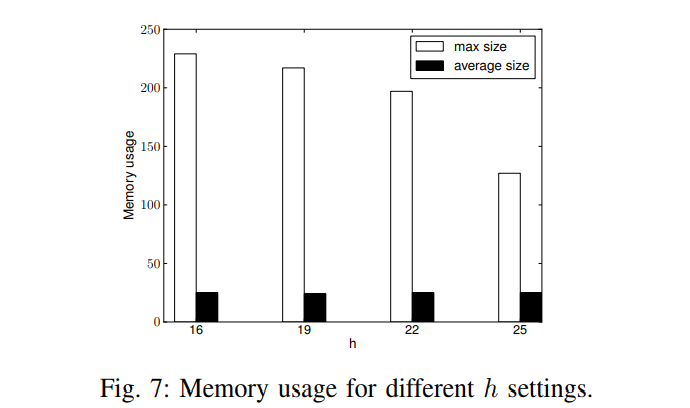
然后作者使用了 $\lambda=512$ ,分别用DL, DS, DR 三种减边策略对网络结构进行了重构,其保留的信息如下:
| Dataset | Original | DL | DS | DR |
|---|---|---|---|---|
| Wiki-Vote | 608389 | 147649 | 55422 | 80455 |
| Cit-HepTh | 1478735 | 776619 | 572934 | 642105 |
| 13082506 | 3284829 | 1693775 | 2210566 |
参数设置中,隐私参数 $\epsilon\in[0.5, 1.5]$,也是一个比较理想的隐私保证。然后我们来看实验结果。
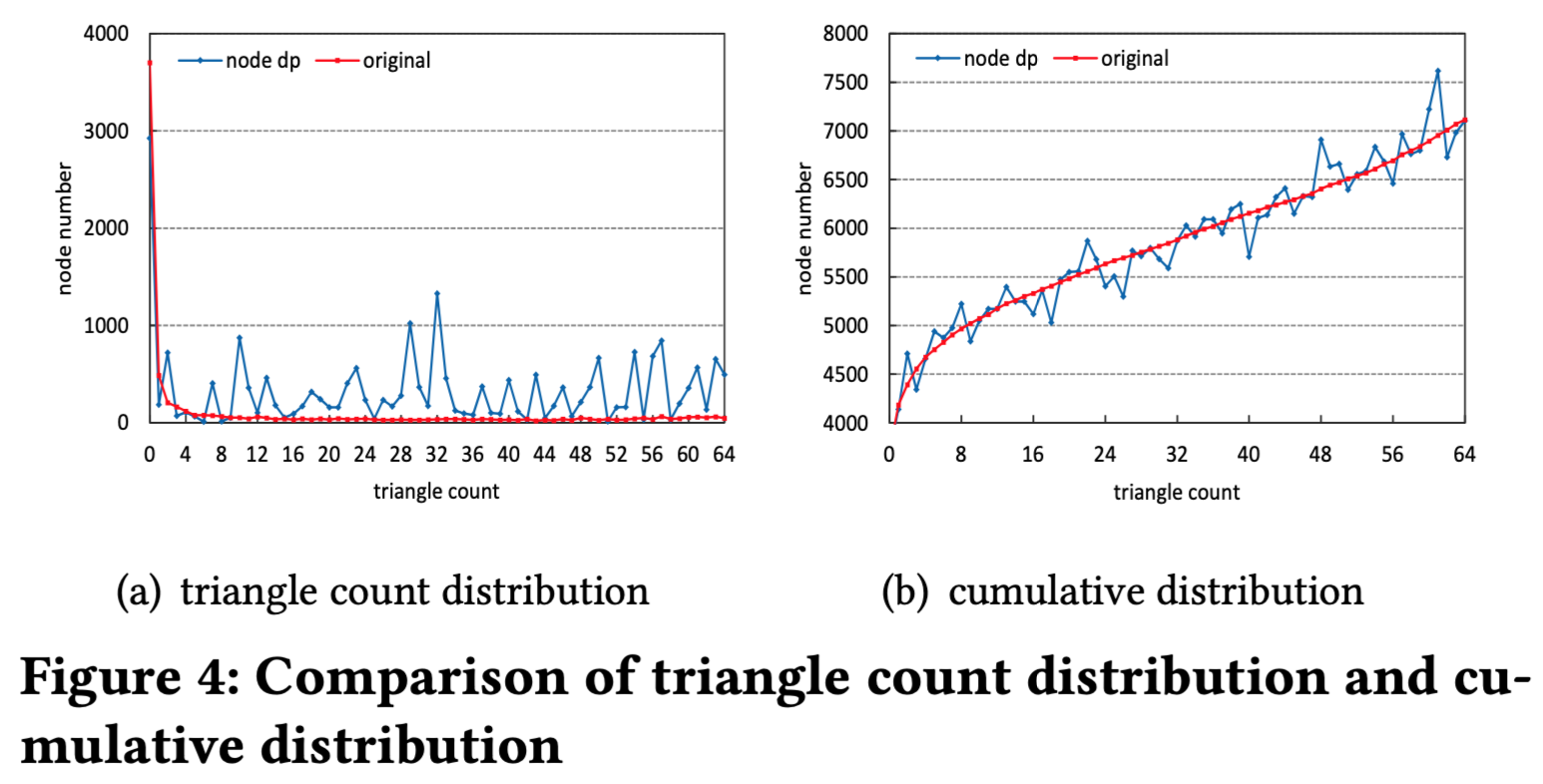
我们先来看一下直方图发布中的实验结果,如图4所示,由于累计直方图中的噪声比直方图中的噪声要小,所以累计直方图相对来说也更接近原始数据。作者的结论就是对于直方图发布来说,累计直方图更能保留数据真实度。

在聚集系数的信息发布中,作者的观点就是聚集系数的直方图发布更能保留数据的真实度。同时作者也发现随着k的增大,误差也会线性变大。这些都也都可以从噪声来源中可以看到。
此外,作者也分析了不同的参数对实验的影响,可以看以下的图: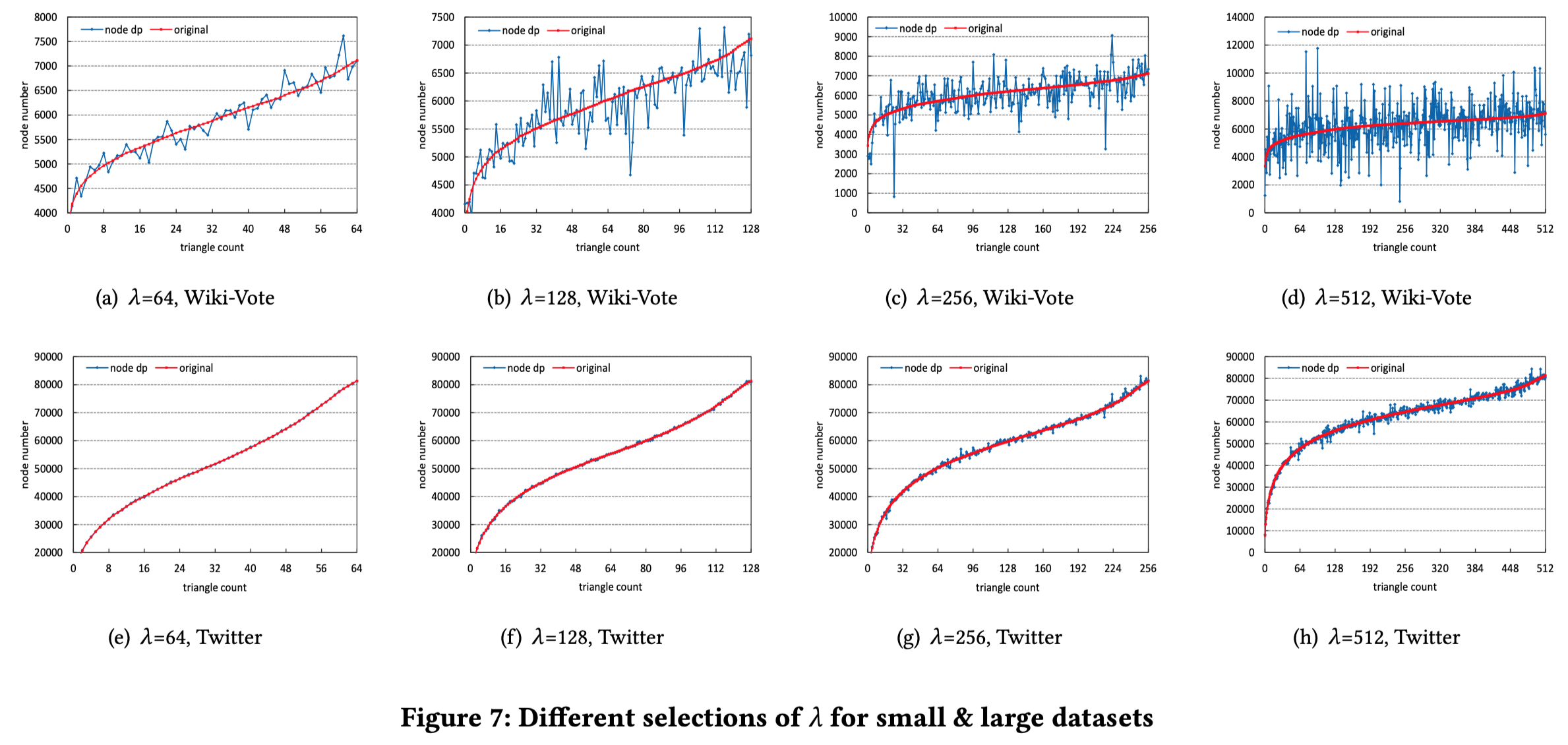
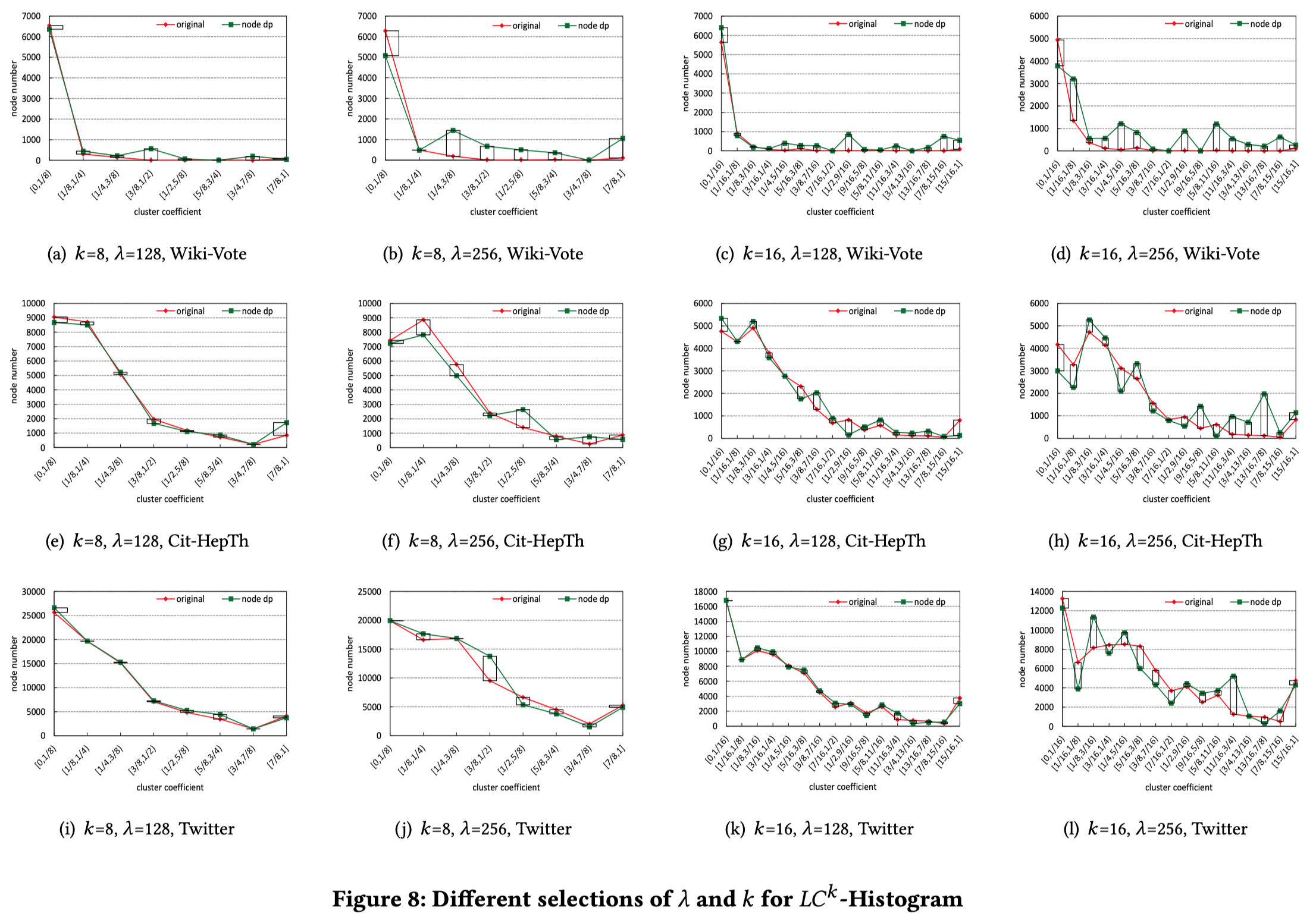
得出的结论也是和上面那几条一样。其实可以发现,效果好的那几个实验基本上都是在twitter数据集上的,因为噪声的大小和节点数目没关,而统计意义上的数的分布就和节点个数有关了。比如噪声是5,节点个数为1,最终的结果为6,感觉6和1偏差很大,但是如果节点个数为500,那么就会觉得500和505差别不大。
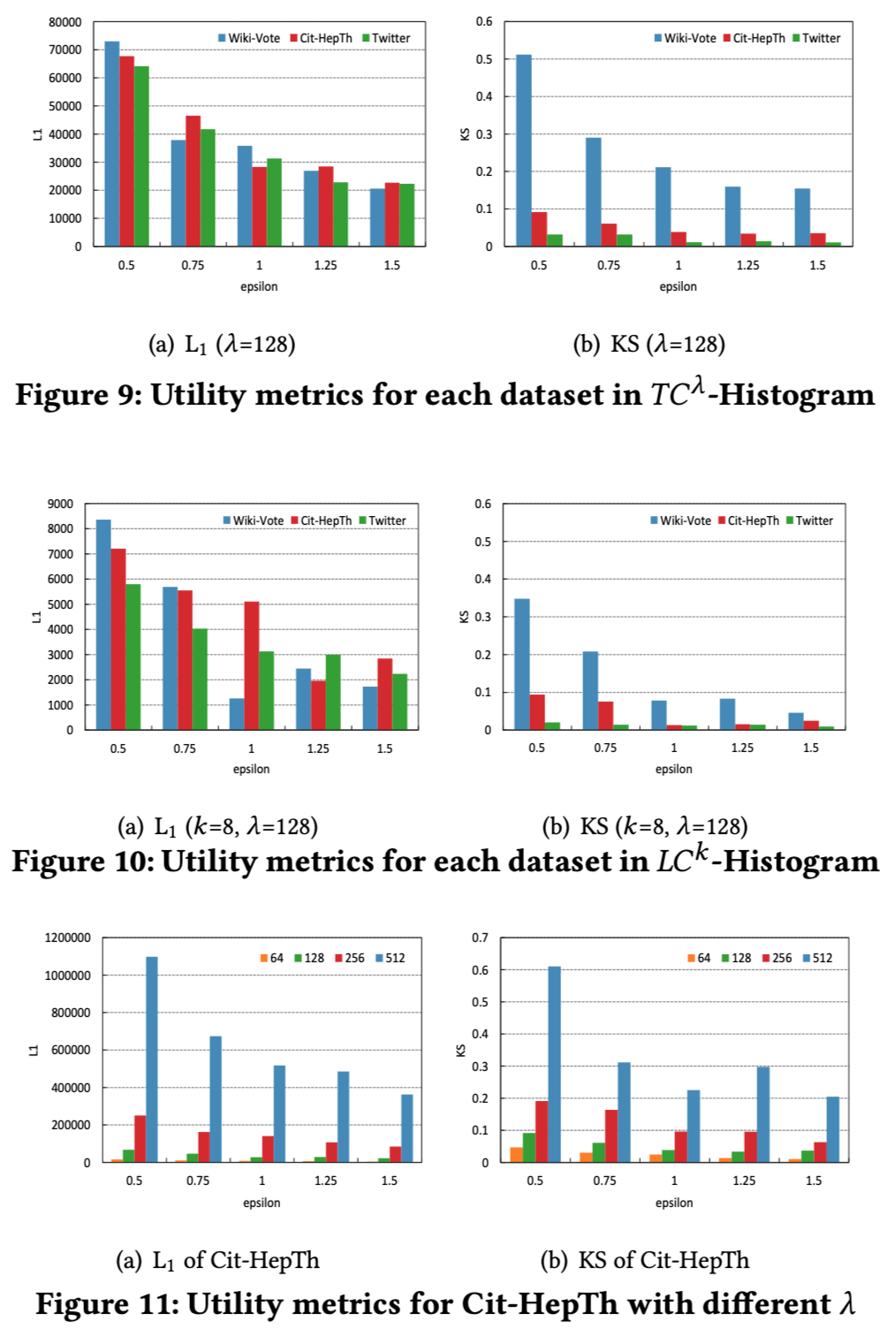
最终作者也分析了Utility metrics,从结果上面来看,结果还是很大的。当然如果单纯为了效果好一点的话可以采用一个小的 λ ,当然我们也知道这是没有意义的,即使数据再好看。因为作者比的Utility 是基于减边之后的比较。
7 Conclusions
总结部分就是把前面的几个工作换了一种表述方法重新说了一遍,在此就不重复说明了。
8 个人反思
理解完这篇文章也花了几天,还好这篇文章没有涉及太多网络结构的背景知识,可以直接读。
首先是在这篇文章中,作者进行了减边处理,然后实验结果都是比较减边之后加上DP对结果的影响。那么问题来了,减边是作者独创的(根据这部分章节在文中的位置,应该是作者的工作),我怎么知道减边对网络结构的影响呢?比如极端情况下,直接设置λ=0,那么接下来的实验会几乎没有误差了,Utility会很高。但是我们知道,减边实际上对网络结构的影响会很大。
其次,在我读这篇文章之前,我认为网络结构中一个节点对网络结构分析的影响应该是比较小的。可是这篇文章中的结果却表明一个节点对直方图数据发布的误差比较大。虽然本文的理论分析确实结果如此,可我仍然觉得一个节点对网络结构影响不大(一只倔强的DPer)。
最后一点,作者的实验部分只是定位于自己提出的方案的实验分析,没有和其他方案的比较,这算是一个缺陷。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


