论文阅读-RAPPOR：Randomized Aggregatable Privacy-Preserving Ordinal Response

文章地址：https://dl.acm.org/citation.cfm?id=2660348
作者：Úlfar Erlingsson; Vasyl Pihur; Aleksandra Korolova
发表会议：Proceedings of the 2014 ACM SIGSAC conference on computer and communications security
目前被引用次数：353(2019.01.07)

---

RAPPOR是一种为终端软件设计的众包统计技术，它支持匿名化，同时带有强的隐私保证，RAPPOR允许服务器端在不知道每个单一数据的前提下对数据整体进行分析。本文描述了RAPPOR,并详细介绍其隐私和效用保证。

下面是本文的笔记，序号和论文中的序号一样，有些地方我觉得对这篇文章的理解不重要，我跳过了，建议先看一下原文再来看我的笔记。

• 1 Introduction
  • 1.1 The Motivating Application Domain
  • 1.2 Crowdsourcing Statistics with RAPPOR
• 2 The Fundamental RAPPOR Algorithm
  • 2.1 RAPPOR Modifications
• 3 Differential Privacy of RAPPOR
  • 3.1 Differential Privacy of the Permanent Randomized Response
  • 3.2 Differential Privacy of the Instantaneous Randomized Response
• 4 High-utility Decoding of Reports
  • 4.1 Parameter Selection
  • 4.2 What Can We Learn
• 5 Experiments and Evaluation
  • 5.1 Reporting on the Normal Distribution
  • 5.2 Reporting on an Exponentially-distributed Set of Strings
  • 5.3 Reporting on Windows Process Names
  • 5.4 Reporting on Chrome Homepages
• 6 Summary

1 Introduction

为了基于数据做出更好、更明智的决策，众包正在被人们所用。对于所有的众包来说，我们应当在众包中运用 Privacy-preserving 的机制来控制数据收集过程中的风险同时平衡收集到的数据的有效性，基于这个出发点作者提出了RAPPOR（Randomized Aggregatable Privacy-Preserving Ordinal Response）。

RAPPOR 建立在 Randomized Response 的基础之上，一个最常见的Randomized Response的情况就是回答是否类的问题，比如”你是不是共产党员“。首先扔一枚硬币，如果正面朝上就老实回答，如果反面朝上就随机回答，随机的过程为再扔一枚硬币，如果另一枚硬币正面朝上就回答是，反面朝上就回答否。

基于Randomized Response的调查可以轻松计算人口的统计结果并且保证单一个人的隐私。假定严格使用Randomized Response机制，并且统计到回答“是”的占比重为Y，则真实的结果中回答“是”的比例为 2(Y-0.5)。从期望上来看，回答者有75%的可能性会保证回答的是真实的。

更重要的是，对于一次数据收集来说，Randomized Response是提供 ln3-DP的，即使攻击者有其他先验信息。当然，随着对同一个个体的重复性回答，隐私保护程度是会下降的。比如对同一个回答者重复问同样的问题。在这种案例下，为了更好地权衡privacy和utility，也需要更好的安全机制，。

RAPPOR是用于统计终端用户的信息的机制，同时保证强的隐私保证。RAPPOR旨在收集大量用户信息，如他们的类别、频率、直方图，或者其他统计信息，同时为用于提供强有力的隐私保护。

一个直接的贡献是再Bloom Filters运用randomized response，RAPPOR允许收集字符串集合的信息，同时带有DP保证。另一个贡献是RAPPOR以优雅的方式保护重复（甚至无限地）收集数据的客户端的隐私。RAPPOR可以避免形式上的隐私保护，比如对同一回答保存一个本地结果并每次响应本地结果（可能是linkable的，并被跟踪到）。相比之下，传统的randomized response机制在同一参与者多个信息收集者的情况下不提供任何隐私保护。另一个贡献是RAPPOR在本地执行，并且不需要任何可信的第三方。

最后，基于假设检验、最小二乘法和LASSO回归，RAPPOR提供了一种新颖的高效用解码框架

1.1 The Motivating Application Domain

RAPPOR是一个众包统计中的保护隐私的综合技术，可以用于很多应用领域中。

然而，在本文中，作者关注促进RAPPOR发展的特定应用领域：云服务运营商需要收集有关其用户活动及其客户端软件的最新统计数据。 在这个领域，RAPPOR已经部署在Google的Chrome Web浏览器中，它已被用于改进用户向谷歌发送的数据。 第5.4节简要描述了这个应用程序，以及RAPPOR通过对不必要或恶意劫持用户设置的方式提供的好处。

出于各种原因，了解人口统计数据是云服务和软件平台运营商的可靠运行的关键部分。理由通常很简单，比如有些软件需要手机对于特定的功能，用户的使用频率。或者收集软件失败的次数。 另一个重要的原因涉及到用户，收集数据可以为用户提供更好的安全保证。举个例子，在评估僵尸网络或者被劫持客户端的流行程度时，运营商希望监控到过去一段时间有多少客户的Web搜索被重定向了。

收集最新的众包统计数据给服务运营商带来了两难境地。 一方面，直接收集他们的信息可能会损害最终用户的隐私。 另一方面，不收集任何此类信息也将对用户造成损害： 如果运营商无法收集正确的统计数据，他们就无法为用户带来许多软件和服务改进（例如，通过检测或阻止恶意的客户端活动）。 通常，运营商通过使用仅限于必要的高阶统计数据的技术来解决这一难题， 例如，仅收集粗粒度数据。

不幸的是，即使对于愿意使用最先进技术的谨慎操作员来说，现有的机制在 utility 和 privacy 之间也很难权衡。 因此，为了降低隐私风险，运营商在很大程度上依赖于一些实用的手段和流程而不是技术保障，比如去掉标志化信息，避免收集某些数据或隔一段时间强制清理数据。即对数据用访问控制和审计策略来保障数据安全。 然而，这些方法在提供可证实的强大隐私保证的能力方面受到限制。 此外，可能会出现来自个人数据集的隐私外部性，例如时间戳或可链接的标识符; 这些外部性的隐私影响甚至可能大于收集的数据。

RAPPOR可以帮助运营商处理由此困境引发的重大挑战和潜在的隐私陷阱。

1.2 Crowdsourcing Statistics with RAPPOR

运用 RAPPOR，数据操作者可以以保护用户隐私的方式解决众包统计问题，从而解决上述关于privacy和utility的问题。

作为简化，可以假设 RAPPOR 响应是bit string（01串），其中每个位对应于报告客户端属性（不失一般性，本假设用于本文的其余部分）。比如其中第一位表示使用者是否为男性，第二位表示使用者是否是共产党员。

RAPPOR 响应的结构是没有限制的，不过需要注意以下几点：

• 响应位可以是顺序的或无序的
• 响应谓词可以是独立的，不相交的或相关的
• 客户端的属性可以是不可变的，或者随时间变化

但是，必须正确考虑这些细节（例如，响应位的相关性），因为它们会影响RAPPOR 的使用和隐私保证 - 如下一节所述，并在后面的章节中详述。

特别是，RAPPOR 可用于收集分类客户端属性的统计信息，方法是让客户端响应中的每个位表示该客户端是否属于某个类别。例如，某一位可能表示客户端是否正在使用软件功能。在这种情况下，如果每个客户端只能使用三个不相交的特征X，Y和Z中的一个，则来自客户端的三位 RAPPOR 响应的集合将允许测量客户端使用这些特征的频率。

RAPPOR 还可用于收集数值和序数值的总体统计量，例如，通过将响应位与不同数值范围的谓词相关联，或者通过报告值的不同对数量值的不相交类别。对于这样的数值 RAPPOR 统计，可以通过收集和利用关于先验和经验分布的形状的相关信息（例如其平滑度）来改进估计。

最后，RAPPOR 还允许通过使用Bloom过滤器[5]收集非分类域或无法提前确定的类别的统计数据。特别是，RAPPOR 允许在字符串上收集基于Bloom-fi lter的紧凑随机响应，而不是在客户端报告匹配一组由操作员预先设定的手工挑选的字符串时报告。随后，这些响应可以与候选字符串匹配，因为它们对于运营商而言是已知的，并且用于估计群体中的已知和未知字符串。必须应用先进的统计解码技术来准确地解释基于Bloom滤波器的 RAPPOR 响应中的随机噪声数据。但是，与类别一样，此分析只需要考虑 RAPPOR 响应中设置的不同位的总计数，以便为人口统计提供良好的估计，详见第4节。

在不损失隐私的情况下，可以在一组响应上重新运行 RAPPOR 分析，例如，考虑在先前分析中遗漏的新字符串和案例，而无需重新运行数据收集步骤。个人回答对于探索性或定制数据分析尤其有用。例如，如果客户的IP地址的地理位置与其敏感值的 RAPPOR 报告一起收集，则可以在不同的地理位置之间比较这些值的观察分布。这种分析与 RAPPOR 的隐私保证兼容，即使在存在辅助数据（例如地理定位）的情况下也是如此。通过限制任何单个客户端报告的相关类别或Bloom fiter 散列函数的数量，即使在客户的多个方面收集统计数据时，RAPPOR 仍可保持 DP，详细说明在第3节和第6节。

The Fundamental RAPPOR Algorithm

接下来我们讲一下RAPPOR的四个关键步骤，为了防止歧义，这里的步骤我直接从摘抄原文，然后再解读。

1. Signal. Hash client’s value $v$ onto the Bloom filter $B$ of size $k$ using $h$ hash functions.
2. Permanent randomized response. For each client’s value $v$ and bit $i, 0 < i < k$ in $B$, create a binary reporting value $B_i’$ which equals to: $$B_i' = \begin{cases} 1 & \text{with probability } \frac{1}{2} f\\ 0 & \text{with probability } \frac{1}{2} f \\ B_i & \text{with probability } 1-f \end{cases}$$ where $f$ is a user-tunable parameter controlling the level of longitudinal privacy guarantee. Subsequently, this $B’$ is memoized and reused as the basis for all future reports on this distinct value $v$.
3. Instantaneour randomized response. Allocate a bit array $S$ of size $k$ and initialize to 0. Set each bit $i$ in $S$ with probabilities: $$\Pr[S_i=1] = \begin{cases} q & \text{if } B_i'=1\\ p & \text{if } B_i'=0 \end{cases}$$
4. Report. Send the generated report $S$ to the server.

我们来看一下这四步做了一个什么事情：

• Signal: 这一步是使用布隆过滤器将一个数字 $v$ 映射到一个比特串 $B$，虽然 Bloom filter 中的哈希函数是不可逆的，但是从 DP 的角度来说，bloom filter是不带隐私保护的。
• Permanent randomized response: 这一步对第一步中的 $B$ 进行处理，得到$B’$，同时 $B’$ 永远代替 $B$。处理的方法就是对第一步的比特串 $B$ 的每一位以 $f$ 的概率随机回答，以 $1-f$ 的概率真实回答。
• Instantaneous randomized response: 对 $B’$ 进行处理，得到 $B’$ 处理之后得到的 $S$。这一步的处理过程和 Permanent randomized response 有点类似，不过概率上有一定的区别。
• Report: 发送产生的结果 $S$。

接下来我们看一个这个的应用案例，假如我们映射的比特串长度是256 ($k=256$)，然后采用了四个哈希函数($h=4$)，控制概率的参数为 $p=0.5, q=0.75, f=0.5$。那么我们看一下这个例子。

• Step.1 数字 68 经过 bloom filter之后，有4位置1。即图1中的$B$
• Step.2 对$B$中的每一位以 $1-f=0.5$ 的概率真实回答，以 $0.5$ 的概率随机回答。相当于以$(1+0.5)/2=0.75$的概率保留原有结果，以$0.25$概率取反。
• Step.3 考虑$B’$的每一位，如果是1则以0.75概率保持1，以0.25概率为0.如果是0，以0.5概率为1，以0.5概率为0。
• Step.4 把最终的结果发送给服务器。

这个过程的安全性我们会在第三节中介绍。接下来我们看一下这个方法的几个分支。

2.1 RAPPOR Modifications

由于不同的应用需求，不一定要使用完整版的RAPPOR，这里，作者把RAPPOR分成了三个简单版本的RAPPOR：

• One-time RAPPOR:
  这个模式针对单次数据收集，如果数据只收集一次的话，那么可以直接跳过Instantaneour randomized response。即跳过第三步。
• Basic RAPPOR:
  如果输入的本来就是一个01串（比如第一位表示男女，第二位表示农村户口还是城市户口…），这种时候就不需要布隆过滤器了。因为布隆过滤器的目的就是将数据映射到01串。
• Basic One-time RAPPOR:
  这是一种最简单的RAPPOR，相当于One-time和Basic的结合，仅仅有一步Permanent randomized response

3 Differential Privacy of RAPPOR

这一节我们分析RAPPOR的隐私性质。

3.1 Differential Privacy of the Permanent Randomized Response

Theorem 1. The permanent randomized response (Steps 1 and 2 of RAPPOR) satifies $\epsilon_\infty$-differential privacy where $\epsilon_\infty=2h\ln(\frac{1-\frac{1}{2}f}{\frac{1}{2}f})$

我们先来看这个定理，这个定理说 RAPPOR 的步骤1和步骤2是满足差分隐私性质的，同时给出了$\epsilon$。文章中的证明用了很多公式，我这里用易于理解的方式描述出来。

先不考虑bllom filter，我们看一个二进制串，如果只有1位的话，那么：

$$\begin{align} &\Pr[0|0]=\Pr[1|1]=1-\frac{f}{2}\nonumber\\ &\Pr[1|0]=\Pr[0|1]=\frac{f}{2}\nonumber \end{align}$$

所以在仅仅有1位的情况下，隐私保护程度为$\ln[(1-\frac{f}{2})/(\frac{f}{2})] $

同样的道理，如果是 $n$ 位的话，那么隐私保护程度应该是 $n \times \ln[(1-\frac{f}{2})/(\frac{f}{2})]$。那么为什么定理1中是 $2h$ 呢。根本原因是由于 bloom filter。在Step.1中，经过 bloom filter 之后，每一个原始值映射到的01串中最多只有 $h$ 个1。所以对于原始输入 $x$ 和 $y$，他们的 bloom filter 的值最多只会有 $2h$ 位不一样（即他们映射到的1的位置完全不一样）所以Step.2是 $2h\ln(\frac{1-\frac{1}{2}f}{\frac{1}{2}f})$-DP的。

当然，这是形式上的理解，数学上的证明过程也是这样，只不过要用数学上严格的记法证明出来。

3.2 Differential Privacy of the Instantaneous Randomized Response

上面只说了Step.2的隐私保护程度，接下来我们再看加上Step.3中的 Instantaneour Randomized Response 的 privacy-preserving 之后的隐私保护等级。

首先还是需要知道原始数据到最终数据的映射概率：

$$\begin{align} q^*=\Pr[S_i=1|b_i=1]=\frac{1}{2}f(p+q)+(1-f)q \nonumber\\ p^*=\Pr[s_i=1|b_i=0]=\frac{1}{2}f(p+q)+(1-f)p \nonumber \end{align}$$

上述两个公式给出了从 $B$ 到 $S$ 的映射概率。因此有了接下来的定理2：

Theorem 2. The Instantaneour randomized response (Step 3 of RAPPOR) satisfies $\epsilon_1$-differential privacy, where :

$$\epsilon_1=h \log \frac{q^{*} (1-p^{*})}{p^{*}(1-q^{*})}$$

Proof: 我们只需要求出两个概率的比值的最大值就好了。

$$\begin{align} e^{\epsilon_1}& =\max_\limits{S} \frac{\Pr[S\in R|B=B_1]}{\Pr[S\in R|B=B_2]} \nonumber \\ &= [\frac{q^*(1-p^*)}{p^*(1-q^*)}]^h \nonumber \end{align}$$

4 High-utility Decoding of Reports

大多数应用需求中，数据收集的目标是需要知道哪些字符串出现在样本群体中以及他们对应的频率。由于在bloom filter中信息是有损失的（哈希函数的空间问题）而且DP也加噪了，所以我们需要更先进的数据统计方法。

我们假定有m个cohorts，为了方便从数据中学到东西，每一个数据源一开始被随机分配到其中一个cohort，并且永久成为这个cohort的一员。每一个cohort之间唯一的区别在于他们在bloom filter中使用了不同的哈希函数（为了降低撞击的概率）。通过同时存在m个cohorts可以提高false positive率。当然m的选择需要仔细斟酌，如果m选在太小了，那么很可能出现撞击，如果m太大了，那么每个cohort的样本数量就会很少（假如总共有 N 个数据，那么每个 cohort 只能收到 N/m 个数据），造成数据分析中出现比较大的误差。当然每个用户在发送数据之前是需要告知自己是属于哪个cohort的。

数据分析的过程如下按照以下几步进行，我先放出原文再写自己的理解：

1. Estimate the number of times each bit $i$ within cohort $j$, $t_{ij}$, is truly set in $B$ for each cohort. Given the number of times each bit $i$ in cohort $j$, $c_{ij}$ was set in a set of $N_j$ reports, the estimate is given by:

   $$t_{ij}=\frac{c_{ij}-(p+\frac{1}{2}fq-\frac{1}{2}fp)N_j}{(1-f)(q-p)}$$

   Let $Y$ be a vecotr of $t_{ij}$’s, $i \in [1,k], j \in [1,m]$

2. Create a design matrix $X$ of size $km\times M$ where $M$ is the number of candidate strings under consideration. $X$ is mostly 0 (sparse) with 1’s at the Bloom filter bits for each string for each cohort. So each column of $X$ contains $hm$ 1’s at positions where a particular candidate string was mapped to by the Bloom filters in all $m$ cohorts. Use Lasso regression to fit a model $Y \sim X$ and select candidate strings corresponding to non-zero coefficients.

3. Fit a regular least-squares regression using the selected variables to estimate counts, their standard errors and $p$-values.

4. Compare $p$-values to a Bonferroni corrected level of $\alpha / m = 0.05 / M$ to determine which frequencies are statistically significant from 0. Alternatively, controlling the False Discovery Rate (FDR) at level $\alpha$ using the Benjamini-Hochberg procedure, for example, could be used.

为了方便理解上面的这个过程，我们假定m=1，即只有一个cohort。我们以单词个数统计为例子更加形象化地解释这个过程，假如我们已经有一个词库，这个词库里面列出了所有的单词，现在想干一件什么事呢？统计每个单词出现的频率。怎么统计呢，就是我收到一个单词，我就记一次。不过麻烦的是现在是在privacy-preserving的情况下做这么一件事情。首先cohort的哈希函数是公开的，这就意味着RAPPOR中的 step.1 实际上是公开的，也就是说服务器端是知道每个单词对应的bloom filter的。

然后我们来看用户（假定用户是很多很多的），每个用户在本地都把自己用到的单词经过Step.2的Permanent randomized response并且保存在本地，所以每个单词就变成了一个01串了，然后每使用一次单词，究竟过一次Instantaneous randomized response并且发送到服务器端。服务器端的工作就是根据收到的01串统计原来每个单词的个数。我们假设只有单词”A”,”B”,”C”，并且：

$$\begin{align} & bloomfilter("A") = 10001000 \nonumber\\ & bloomfilter("B") = 01000010 \nonumber\\ & bloomfilter("C") = 00010010 \nonumber\\ \end{align}$$

当然，由于服务器知道哈希函数，所以服务器是知道上面的bloomfilter的。

再看用户，首先每个用户都对自己的单词进行Step.2，然后得到了新的8位01串替换掉原来bloomfilter，然后每次使用的时候在根据Step.3临时产生一个01串发送到服务器。

作为服务器是怎么统计词频的呢？实际上服务器先收集了每一位上1的个数，一共k位。所以一组数据肯定会对应k个数据，每一个数据表示第 i 位的求和。还是以我们的数据为例，加入出现AABC，那么原始的对应8位数就是

$$\begin{align} & bloomfilter("A") = 10001000 \nonumber\\ & bloomfilter("A") = 10001000 \nonumber\\ & bloomfilter("B") = 01000010 \nonumber\\ & bloomfilter("C") = 00010010 \nonumber\\ & T = 21012020 \nonumber\\ \end{align}$$

我们想要通过收集到的数据分析出来的也就是这个 $T$ 了，我们再来看怎么分析出这个 $T$。由于每一列都是独立的，所以可以只分析一列。假设原来的第一位有$x$个1，则有$N-x$个0。按照Step.2和Step.3之后，我们看服务器端平均来说会收到多少个1。我先把原来的概率列出来：

$$\begin{align} q^*=\Pr[S_i=1|b_i=1]=\frac{1}{2}f(p+q)+(1-f)q \nonumber\\ p^*=\Pr[s_i=1|b_i=0]=\frac{1}{2}f(p+q)+(1-f)p \nonumber \end{align}$$

所以服务器端平均收到的1的个数为：

$$y = x\cdot q^{*} + (N-x)\cdot p^{*}$$

解这个式子就可以得到：

$$y = \frac{y-N\cdot q^{*}}{q^{*}-p^{*}}=\frac{y-(p+\frac{1}{2}fq-\frac{1}{2}fp)\cdot N}{(1-f)(q-p)}$$

也就是论文中的式子了，只不过我把字母写成了$x,y$。

这就意味着仅仅通过数学计算我就可以估计出输入的原始值中每一位当中1的个数了。在我们这个例子中，也就是知道了T = 21012020。那么我们再来看，知道了T之后还可以干什么呢，回顾一开始的假设，我们知道bloomfilter的，也就是说我们现在知道的其实是：

$$\begin{align} & bloomfilter("A") = 10001000 \nonumber\\ & bloomfilter("A") = 10001000 \nonumber\\ & bloomfilter("B") = 01000010 \nonumber\\ & bloomfilter("C") = 00010010 \nonumber\\ & T = 21012020 \nonumber\\ \end{align}$$

所以肯定知道有2个 A，一个 B 和一个 C 啊。不过注意，这里的 T 我们只能大致估计，不一定完全准确，所以我们需要用机器学习的方法拟合出到底每个单词有多少个是最恰当的。这也就是第二步第三步做的事情了。第四步中的p值是统计中的概念了，可以自行查阅一下。

4.1 Parameter Selection

RAPPOR在现实场景中运用的时候需要用到很多参数，比如概率 $p, q, f$ 以及 $h$ 都和 privacy 相关（个人觉得 $h$ 和 privacy 不是太大关系，至少没有理论上的联系）。如果没有长期数据收集的话，只需要用One-time RAPPOR就可以了。$p, q, f$ 都和DP的 $\epsilon$ 相关，$\epsilon$ 的选取可以根据数据收集的具体情况看。$k, m, h$ 的选取就需要一定的先验知识了。

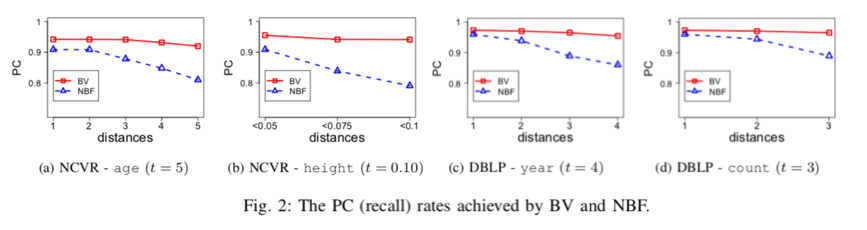
设定 $\epsilon=\ln 3$，作者运行了一部分实验。实验中每个用户只传输一次值，所以作者使用 One-time RAPPOR。作者用了100个出现概率的字符串和100个不出现的字符串来模拟，出现了的字符串概率分布是服从指数分布的，就是下面四个图中的第一个图所示。其他图中展示了 recall 和 precision 的关系。作者做完实验后说，参数的选取很困难。对于参数选取，作者也给不了什么意见~。

PS：这里的 recall 和 precision 文中没有完全说清楚如何计算，我猜测是只是看有没有找出来这个串存在不存在，而不是看估计的串的个数和实际串的个数是否一样。

4.2 What Can We Learn

上图中横坐标表示样本大小，纵坐标表示在该样本数量上可以检测到的字符串个数的理论上界，参数设置为 $p=0.5, q=0.75, f=0$，置信度 $\alpha=0.05$。而且结果发现随着数据量的增大，对于频率比较低的字符串就会难以检测到。

同时作者还给出在样本量为N的情况下，可以检测到的大致为 $\sqrt{N}/10$ 个串。这个结果是基于Basic One-time RAPPOR计算出来的。理论的计算作者放在了附录，感兴趣的可以参考原文。

虽然在One-time RAPPOR中使用了ln(3)的隐私保护成都，识别频率为1%的串需要至少1000000样本，而识别出频率为0.01%的串则需要超过10e9的样本大小。

作者还发现与Basic One-time RAPPOR相比较，RAPPOR效果要下降的更多，毕竟RAPPOR提供了更高的隐私保护成都。当然，如果假定数据分布均匀的话，即使是RAPPOR，上面的结论也可以计算出来。

总的来说就是频率低的串不太容易被检测出来。

5 Experiments and Evaluation

5.1 Reporting on the Normal Distribution

有了上面的分析之后这个实验就很显然了，作者学习了正态分布，使用的是Basic One-time RAPPOR，这里从论文中我也依然没懂数据是如何表示的，因为Basic One-time RAPPOR是没有bloom filter的，理论上我感觉效果会比有bloomfilter的好。是二进制表示数据吗？还是更暴力的方法，比如1就表示为0100000…，2表示为0010000…，每一位表示一个数据的话我感觉准确率会更高。

5.2 Reporting on an Exponentially-distributed Set of Strings

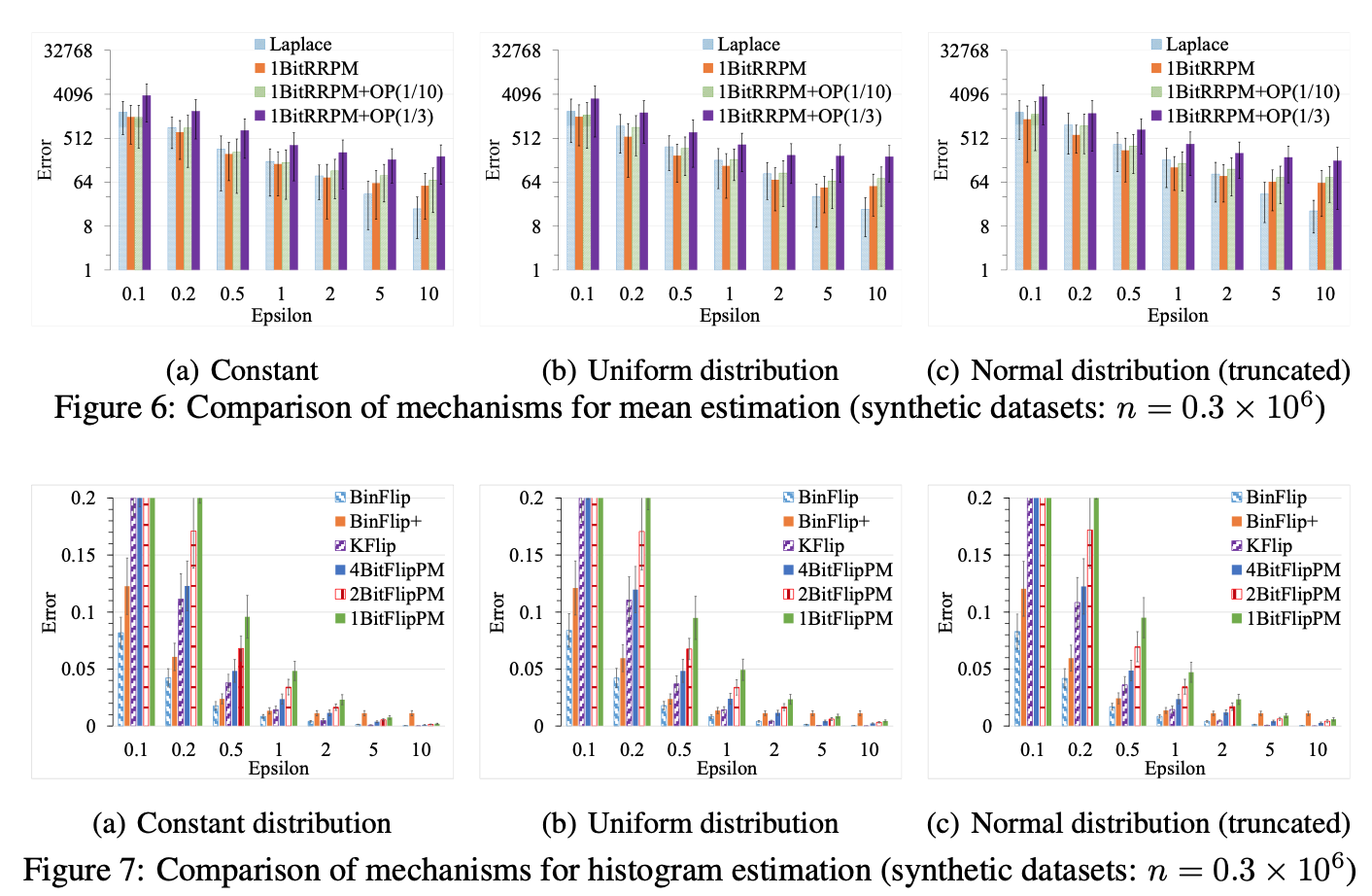
作者还做了指数分布的实验，至于为什么有正态分布还继续做指数分布我猜测可能是指数有个长尾效应，做这个实验更加说明检测不到频率低的。图5红色的说明检测到了，白色的说明没有检测到，这个实验更加说明了频率低的难以检测。当然检测到了并不能说检测的就对，还要看检测的个数准不准。

所以作者又把TOP-20的计算结果和真是结果来对比，下表给出了估计的个数，和实际的差，p值和z-scores(SNR)值等。

看上去感觉挺准的，不过我们也知道这个方法的最主要问题在于低频串的识别，找TOP-20自然是比较准的。

5.3 Reporting on Windows Process Names

作者还监控了Windows进程调用的实验，看哪些进程被调用，作者从10138个不同的计算中收集了186792此进程调用反馈，然后来找一个叫 “BADAPPLE.COM” 的恶意库（这一看就是在黑苹果啊，我还特意回头看了一下，作者是谷歌的，难道因为苹果说在iOS里面用了DP？）然后也列了前几个找到的结果：

5.4 Reporting on Chrome Homepages

当然，在黑了一下苹果之后，谷歌的东西自然要落地到谷歌的产品中。为了表示一下谷歌是多么为用户考虑，文中特别强调了作者收集的数据都是用户在使用谷歌浏览器的时候同意了向谷歌发送数据的。

住居的手机过程使用128位的bloom filter, 然后概率参数设定为 q=0.75, p=0.5, f=0.75，这就意味着 ε=0.5354。实验之后，作者发现他们找到了31个意料unexpected 的主页，这个unexpected我也不知道怎么理解了。着31个中不是所有的都是恶意的。这个实验的细节还是参考一下原文吧。

6 Summary

RAPPOR是一个灵活、数学严谨、实用的匿名数据收集框架，用于保护客户端数据上的人口统计信息的隐私。RAPPOR通过提供差分隐私保证处理来自同一客户端的多个数据收集。高度可调的参数允许根据个人需求很好地平衡privacy和utility。RAPPOR是基于客户端的隐私解决方案。它消除了对可信第三方服务器的需求，并将客户数据的控制权交还给了自己的手中。

文章中的问题

我觉得作者忽略了一个很重要的问题就是bloom filter之后，串之间很可能是线性相关的，虽然没有说作者有这么个假定，但是如果线性相关的话就会导致有些串会完全估计不出来。举个例子，假如是bloom filter是4位。

$$\begin{align} & A = 1010 \nonumber\\ & B = 0101 \nonumber\\ & C = 1001 \nonumber\\ & D = 0110 \nonumber\\ \end{align}$$

那么知道每一位是1111之后，是无法知道原始数据是AB还是CD的。

---

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。