DP-Gaussian Mechanism

• Gaussian Distribution
• 高斯机制
• 高斯机制的证明

高斯分布 (Gaussian Distribution) 其实就是我们常见的正态分布 (Normal Distribution)，这也就是为什么我们一般都用字母 $\mathcal{N}$ 来表示高斯噪声，而没见过用 $\mathcal{G}$ 去表示的。

若随机变量 $X$ 服从一个位置参数为 $\mu$，尺度参数为的正态分布，记为：

$$X \sim \mathcal{N}(\mu, \sigma^2)$$

其概率密度函数为：

$$f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}}$$

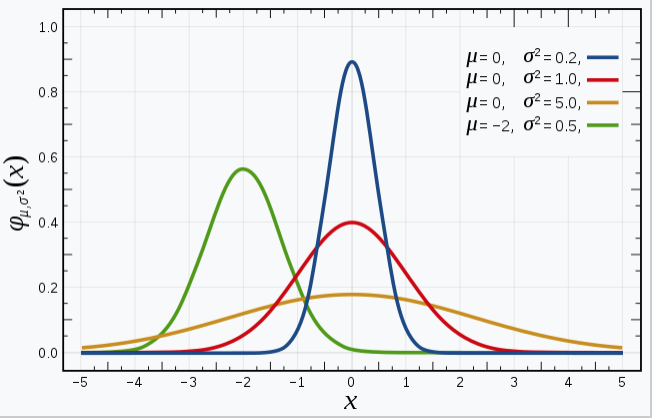
正态分布的数学期望值为 $\mu$，其等于位置参数，决定了分布的位置，其标准差等于尺度参数 $\sigma$，决定了分布的幅度。大家都见过，正态分布都长这样。

Let $\epsilon \in (0,1)$ be arbitrary. For $c^2 > 2\ln (1.25/ \delta)$, the Gaussian Mechanism with parameter $\sigma\ge c\triangle _2f / \epsilon$ is $(\epsilon,\delta)$-differentially private.

说人话的话就是：

给定 $\epsilon \in (0,1)$，如果 $c$ 满足 $c^2 > 2\ln (1.25/\delta)$，那么满足$\sigma\ge c\triangle _2f / \epsilon$ 的高斯噪声是满足 $(\epsilon,\delta)$-DP的.

接下来我们来看看怎么证明这个高斯机制：

对于数据集 $D$ 和查询 $f$，高斯机制返回 $M(D)=f(D)+\mathcal{N}(\sigma^2)$。我们假定我们所说的是实值查询，那么有：

$$\triangle f = \triangle_1f=\triangle_2f$$

然后我们再看和DP有关的证明过程：

$$\begin{align} &\max_{o,D_1,D_2}\frac{\Pr[M(D_1)=o]}{\Pr[M(D_2)=o]} = \frac{\Pr[f(D_1)+\mathcal{N}=o]}{\Pr[f(D_2)+\mathcal{N}=o]}\\ &= \max \frac{\Pr[\mathcal{N}=o-f(D_1)]}{\Pr[\mathcal{N}=o-f(D_2)]}\\ &= \max \frac{\Pr[\mathcal{N}=x]}{\Pr[\mathcal{N}=x+\triangle f]}\\ &= \lvert\frac{e^{-\frac{x^2}{2\sigma^2}}}{e^{-\frac{(x+\triangle f)^2}{2\sigma^2}}} \rvert \end{align}$$

回归到 $\epsilon$，即

$$\epsilon_\infty = \lvert -\frac{1}{2\sigma^2} (2x\triangle f+(\triangle f)^2)\rvert$$

所以当 $x\le \sigma^2\epsilon / \triangle f-\triangle f / 2$ 时，这个重要的公式的上界就是 $\epsilon$ 了，专业一点就是说这个公式就 bounded by $\epsilon$。