论文阅读-A Utility-optimized Framework for Personalized Private Histogram Estimation

发表于 | 更新于 | 分类于 | 阅读次数：

标题：A Utility-optimized Framework for Personalized Private Histogram Estimation
作者：Yiwen Nie, Wei Yang, Liusheng Huang, Xike Xie, Zhenhua Zhao, Shaowei Wang
发表会议：TKDE 2019

本文的主要框架如下：

  • Introduction
  • System Overview
    • Problem Definition
    • Basic Model
    • Utility Metrics
  • Advanced Combination Scheme
    • Scheme Description
    • Theoretical Analysis
  • Data Recycle with Personalized Privacy
  • Recycle Combination Framework
  • Experiments
  • 个人总结

Introduction

在之前的和LDP有关工作的讲解中，一般都有一个全局的 $\epsilon$ 然后所有的用户都是采用的此因此保护程度来保护自己的数据。然而在现实生活中，不同的用户可能拥有不同的隐私保护需求，可能有的用户觉得他需要一个更高的隐私保护程度，而有的用户觉得自己的隐私保护程度不重要，提供更精准的服务才重要。所以本文中用的是 Personalized Differential Privacy ，那么有了不同的epsilon之后如何进行直方图估计就是一个挑战了。

此外，另一个问题就是，我们以往往往将数据收集者和数据分析者放在一起考虑（实际上也确实是的，LDP提出就是不考虑谁拿到数据以及拿到数据的人要干啥）。这篇论文就考虑了假如有不同等级的数据分析者怎么办，即数据收集者需要收集数据，并作出直方图给不同等级的数据分析者，数据分析者只能根据自己的隐私等级接收到相应的隐私等级的数据。这种时候该怎么去解决这个问题。

那么这篇文章讲的什么呢，主要讲的内容可以用一句话总结：This paper studies how to optimize the utility of estimated histograms while considering the personalized privacy requirement of users and diverse credibilities of analysts. 翻译过来就是研究了在用户不同隐私保证程度下及分析者不同可信等级下如何优化直方图估计的效果。

System Overview

Problem Definition

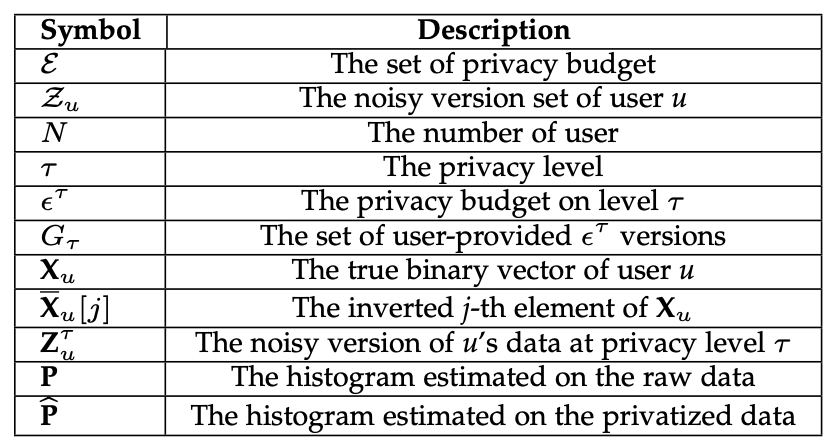
tbl01

我们假定隐私保护程度分为 $m$ 个等级，为$\mathcal{E}=\cup_{\tau=1}^{m}\left\{\epsilon^{\tau}\right\}$，其中 $\epsilon^{\tau}$ 表示等级 $\tau$ 的隐私保护程度。等级越高表示隐私保护越严格（我们认为等级1最严格），因此这也意味着 $\Delta_{\epsilon}=\epsilon^{\tau+1}-\epsilon^{\tau}>0$。

对于直方图来说，我们假设一共有$k$种情况，即直方图可以表示为：$\mathcal{T}=\left\{t_{1}, t_{2}, \dots, t_{k}\right\}$。因此每一个数据都是由01构成的，都长这样：$e_{1}, e_{2}, \dots, e_{k} \in\{0,1\}^{k}$。

同时，我们假定有 $N$ 个用户，每个用户都有一个值：$\mathbf{X}_{u}=\boldsymbol{e}_{j}(u \in[1, N] \text { and } j \in\{1, \ldots, k\})$，并且每个用户都选择了一个隐私保护等级 $\tau$，每个用户都把自己的数据处理之后，发送处理的数据和等级 $<\mathbf{Z}_{u}^{\tau}, \tau>$ 给数据收集者。

总的来说，流程下图所示。

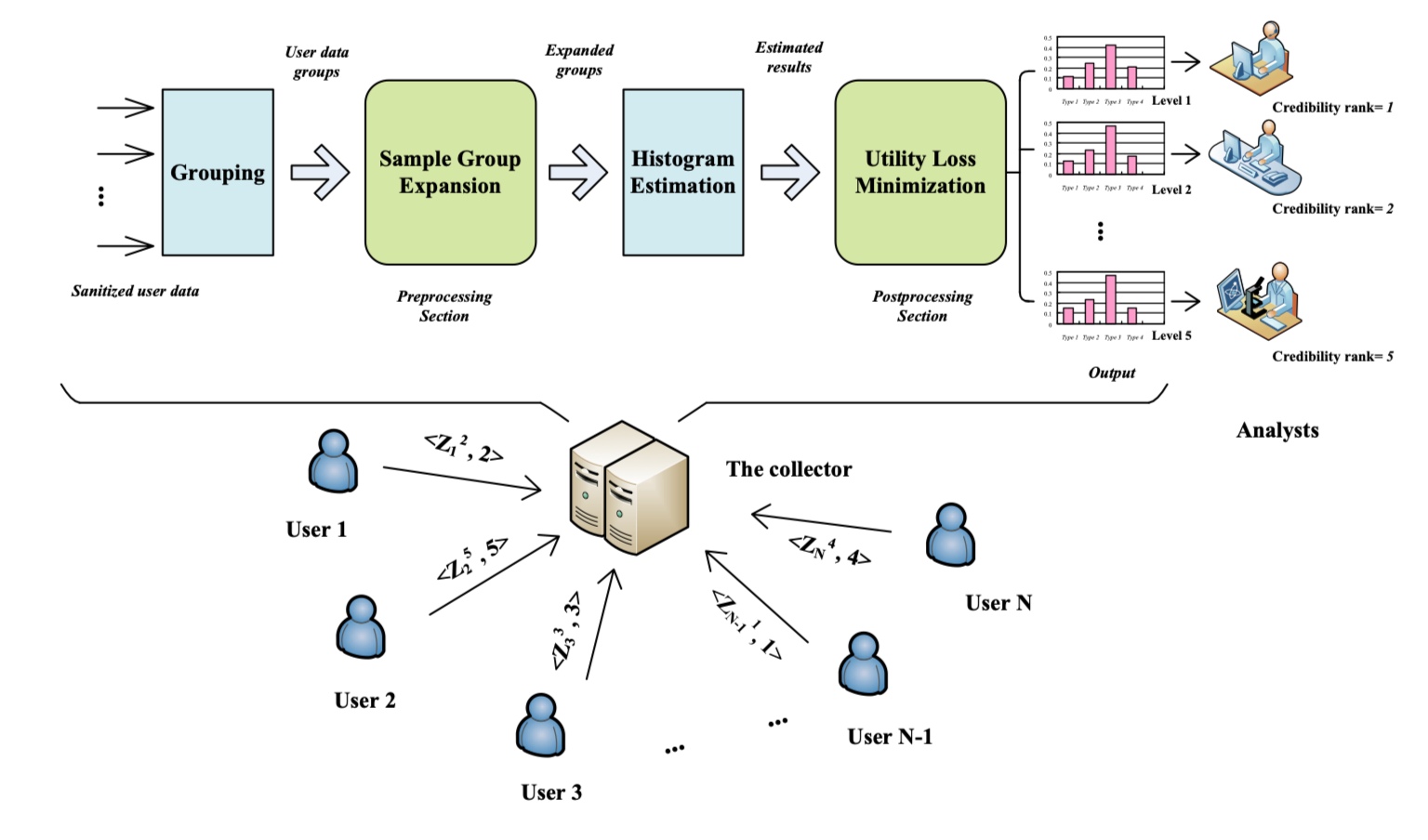
fig01

Basic Model

关于直方图估计，最基本的模型就是算法1和算法2所示了。

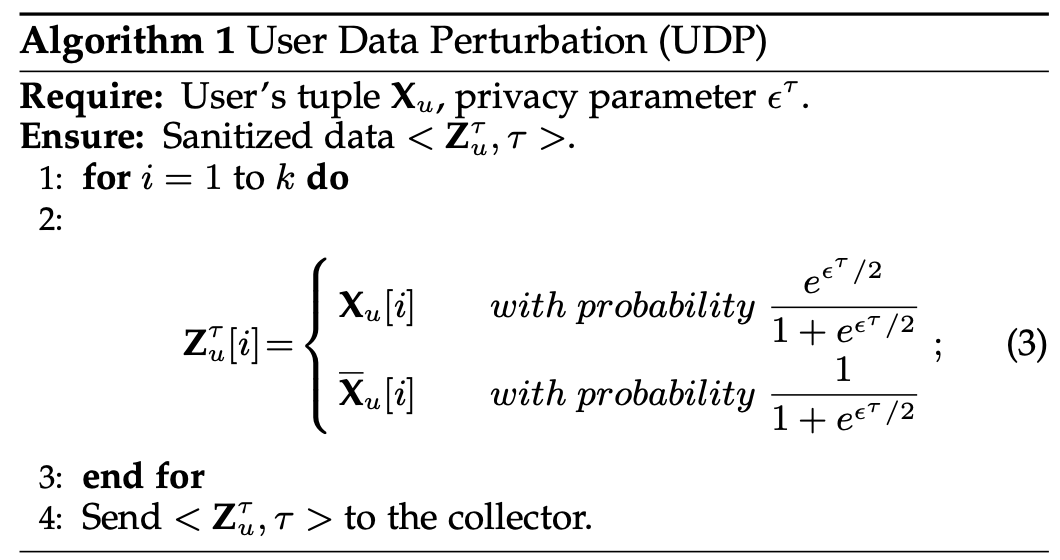
alg01

alg02

算法1介绍了满足$\epsilon$-LDP的编码过程，算法2是根据算法1的编码结果进行的直方图估计。这个算法也被用到了接下来的算法中，由这个算法产生的数据称为 primitive groups，这个算法就被称为PG。

Utility Metrics

那么我们怎么衡量算法的有效性呢，我们采用了 bias 和 Mean Square Error，定义如下：

其中 $\widehat{\mathbf{P}}$ 和 $\mathbf{P}$ 表示估计的直方图和真实的直方图。然后 $|| \cdot ||_2$ 表示2范数。

Advanced Combination Scheme

由于现在对于用户有$m$种隐私保护等级可以选，所以现在的问题来了，怎么根据不同的隐私保护等级去估计直方图呢？最基本的思路是这样的，首先我们把隐私保护一样的分组放在一起，这样就有了 $m$ 组数据，然后每组数据分别去估计一个直方图，所以我们就有了 $m$ 个估计的直方图了。接下来的问题是怎么把这 $m$ 个直方图拼到一起。当然，求平均是一种方法，不过能不能有更好的方法呢？

Scheme Description

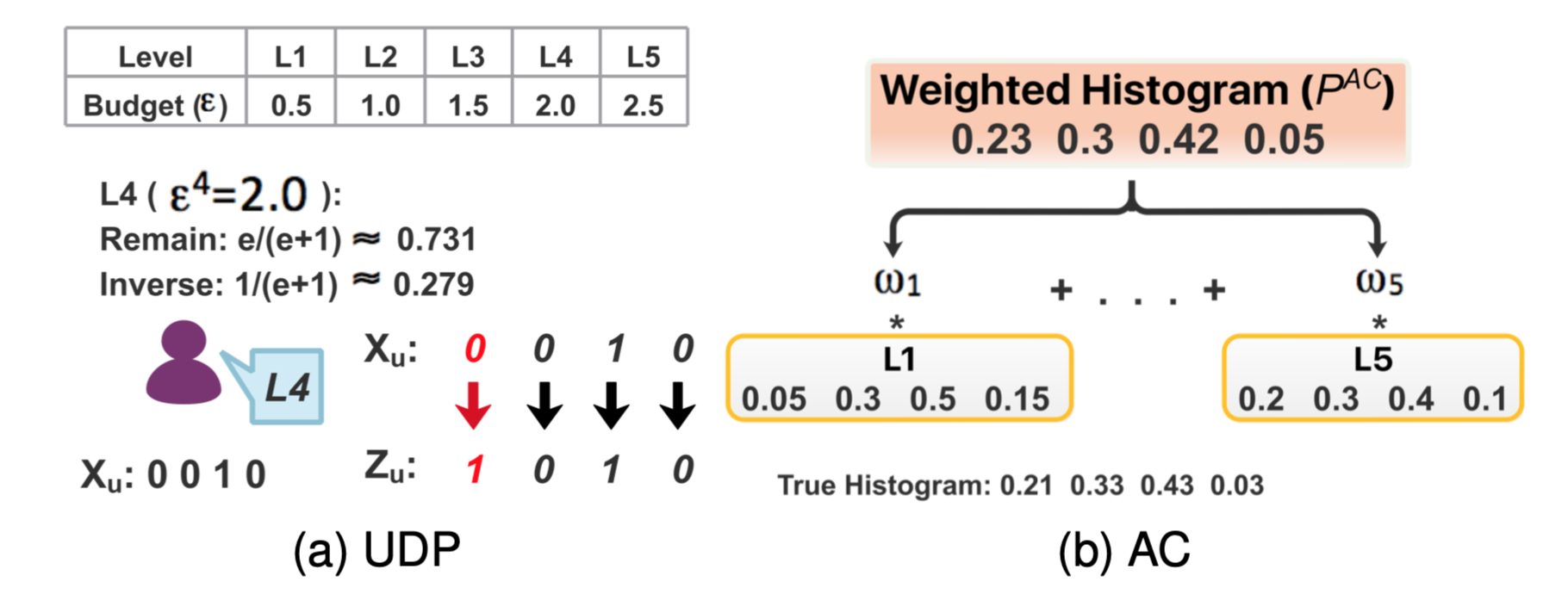
fig02

这个图中的0.279有误，应该是0.269。

因为现在我们已经有$m$个估计的直方图了，即我们有：$\mathcal{P}=\left(\widehat{\mathbf{P}}_{1}, \ldots, \widehat{\mathbf{P}}_{m}\right)^{\top}$。我们想到了给每类直方图设置一个权重 $\boldsymbol{W}=\left(\omega_{1}, \ldots, \omega_{m}\right)$，这样最终的直方图就可以表示为：$\widetilde{\mathbf{P}}=\boldsymbol{W} \mathcal{P}$。我们当然希望这个估计的直方图很接近原始的直方图，所以我们用RSS直接表示出误差（其实就是平方误差），为：

既然有了这个思路，我们何不直接用回归的方法给出参数$\boldsymbol{W}$呢？这里作者给出来了，我没有细算，结果为：

这个算法作者称为 Advanced Combination 算法，缩写为AC。如算法3所示。

alg03

为了方便理解，算法里面的 $d$ 可以直接认为是 $m$。

Theoretical Analysis

有了这个算法之后，必然要进行一番令人头疼的分析。首先，很显然这个方法是满足LDP的要求的，其次，也很显然$\widetilde{\mathbf{P}}$是$\mathbf{P}$的无偏估计。现在重点是怎么求出这个误差，以及证明这个权重的设定会让误差最小。

首先，作者说，这个估计的直方图 $\widetilde{\mathbf{P}}_{d}$ 的MSE误差是：

至于证明过程，因为目前不是特别需要复现一遍，就没有自己尝试证明了，不过证明过程不难。

注意我们的目标是使得估计的误差尽可能地小，实际上 $RSS(\mathbf{W})$ 的期望就是$MSE\left(\widetilde{\mathbf{P}}_{d}\right)$ 嘛。所以我们最小化以下目标就好了：

其中，$B=1-\sum_{j=1}^{k} p_{j}^{2}$。然后作者为了最小化这个目标，给出了算法3中的参数。大致过程是算出了误差函数之后，对权重求偏导使得导数为0就可以了。实际上这个过程就是最小二乘法。

Data Recycle with Personalized Privacy

这时候，我们需要重新审视一下原来的模型了。我们以往说的User发送数据，Aggregator收集分析数据，但是，在图1中，却有三个实体：Users, Collector, Analysts。而且，这里的Analysts是有等级的。

fig01

实际上，考虑到分析者也是有等级的，流程一般是这样的：

  1. Users把自己的数据进行替代，并将发送自己的隐私等级和替代后的数据。
  2. Collector收集所有数据，并对每个等级的数据生成一个直方图。
  3. Collector向不同等级的Analysts发布对应等级的直方图。

那么这里有问题了，我们假设隐私保护有五个等级分别是L1,L2,L3,L4,L5。其中L1等级最高，对应的 $\epsilon$ 也最小。与此对应Analysts也有五个等级。那么很显然，L1的数据给L4的分析者是没有问题的，但是L4的数据不能让L1的分析者看到。即高等级的数据对低等级的分析者可见。有了这个假设之后，我们回头看算法3，算法3实际上是要发布等级d的直方图，那么等级比d大的数据就不能进行使用，所以$d+1\sim m$的权重都设为了0。

Data Recycle的核心思想就是，能否让低等级的数据参与高等级的分析呢？注意，这里只是让低等级的数据去参与高等级的直方图统计，实际上对于Collector说仍然是低等级的（因为Post-processing），只不过通过Collector，使得其对于Analysts来说是高等级的。

论文里面提了三种情况：

  • Case1：同等级 $\rightarrow$ 同等级
  • Case2：低等级 $\rightarrow$ 高等级
  • Case3：高等级+低等级 $\rightarrow$ 中等级

Case1：当然很简单，不用变化啥。

Case2：这里所说的就是讲低等级的数据变成高等级的数据。怎么变呢？方法很简单，在收到的结果上再进行一次Random Response。（BTW，这个方法早在RAPPOR中就已经使用过了。）所以Collector需要对收到的数据进行进一步混淆。概率的公式以后用到的时候再推吧，仅仅用论文中的例子说明。

图2中，用户的原始数据是$X=0010$，这是用户的等级是L4，因此控制Random Response的概率是$e/(e+1)=0.731$，以这个概率作用在$X$上，得到了$L4:1010$。我们现在希望通过L4得到L2的数据。假设在L2上Random Response的概率是$p$，那么应当满足：

这里就可以解得：$p = 0.765$了。根据这个道理，可以把任意低等级的数据变成高等级的数据。

Case3：假如我们现在已经把L4的数据变成了L2的数据了，现在有需要L3的数据，我们该咋办呢。就需要分两种情况了，第一种情况就是如多对应位L4和L2的结果都是一样的，那么就以一定的概率Random Response就行了。如果对应位上面L4的结果和L2的结果不一样，那么以一定概率选择L4的，以一定概率选择L2的就行了。

这中间概率的设计还挺复杂的说。仔细算的话应该也难不倒读者，就不列了。（感觉不久之后还是需要算，到时候算了的话我就再补过来。）所以现在的流程大概是这个样子了：
fig03

知道了Data Recycle的理论之后，算法也就很容易了。

alg04

alg05

所以利用了Data Recycle之后，简单的来说就是高等级分析的数据多了，作者列了个表给我们看看：

tbl02

本来L1,L2,L3,L4,L5,L6分别只有5000，2700，800，900，500，100条数据的，搞个DR之后，很明显高等级的数据就变多了~实际上，每一级的数据就是等级不高于其的数据之和啦。因为低等级都变成了这个等级。

读者可能想，这么一想美滋滋，高等级数据能不能变成低等级呢？不用想了，当人家Post-Processing开玩笑的呢，这要高等级还变成了低等级，低等级再变成高等级，还要无限生成数据不成。

Recycle Combination Framework

alg06

有了生成数据的方法之后，自然而然，我们就可以再根据前面提到的优化方法来优化直方图了。大概思路就是先生成一遍数据，再用直方图估计，再根据估计的结果校正直方图。算法如算法6所示。这个方法作者称为RCF。作者也提到了一种扩充数据的方法就是根据Composition Theorem，基于这种扩充数据方法的直方图估计方法称为ANE。

Experiments

数据集方面，采用了Job数据集和Citizen数据集，前者有45,211条记录，每条记录有12个值，后者有500,000条记录，每条记录有4个值，Epsilon方面，设置了是个等级，间隔分别是0.1和0.5。即如果$\triangle=0.5$，那么隐私等级就是 $[0.5, 1, 1.5, …, 5]$ 这个样子。然后在人群对于隐私程度的选择方面用了两种策略，分别是Uniform和Gaussian，在Uniform情况下，每种隐私等级的人数差不多，Gaussian下，大部分人选择了中间的隐私等级。

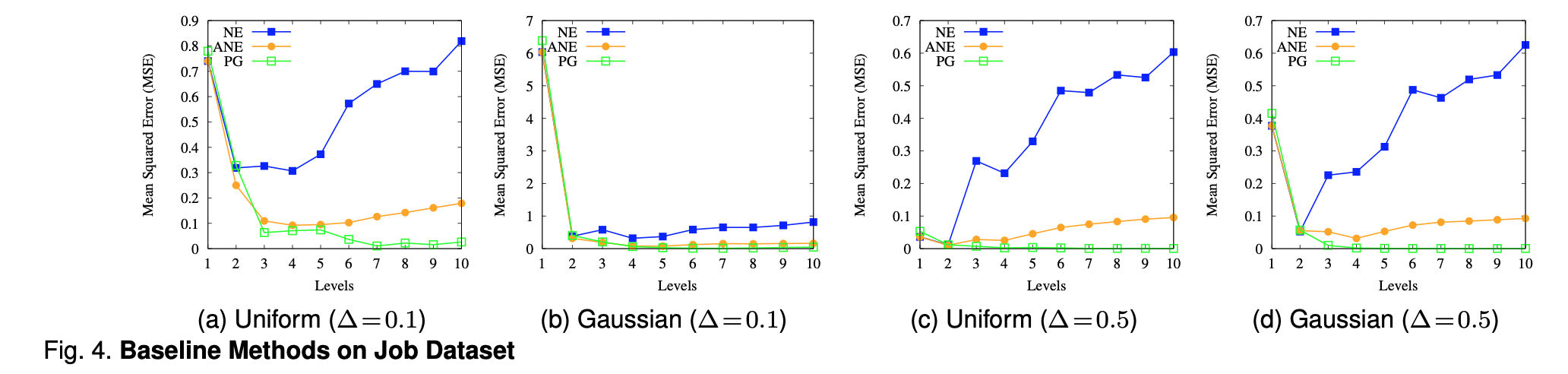
fig04

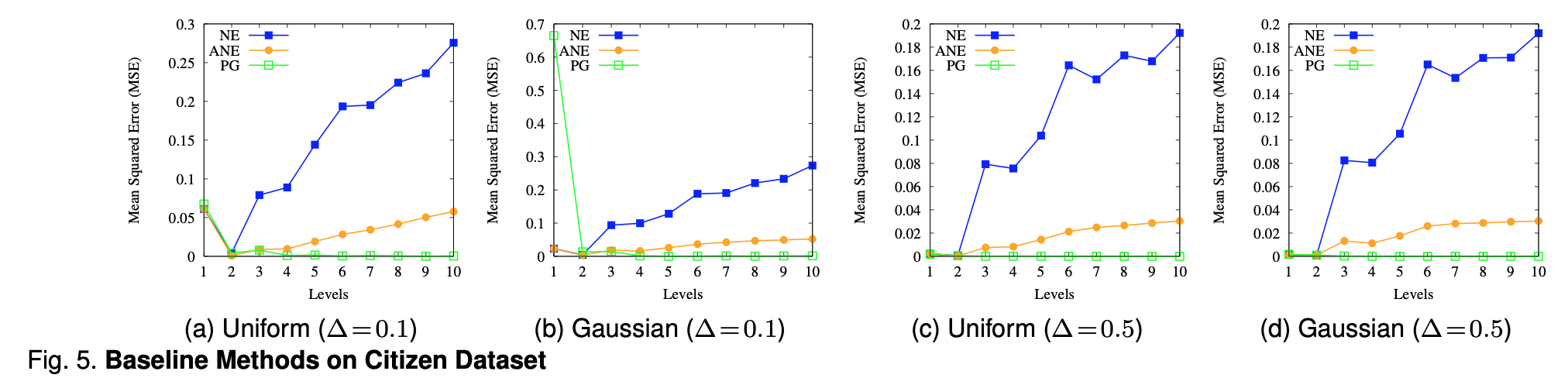
fig05

首先，上面的图4和图5表示了NE,ANE,PG在Job数据集和Citizen数据集上的表现。作者先看了一下NE方法对top level的数据没有太多改进，并且对于低等级的数据还引入了较大的误差。

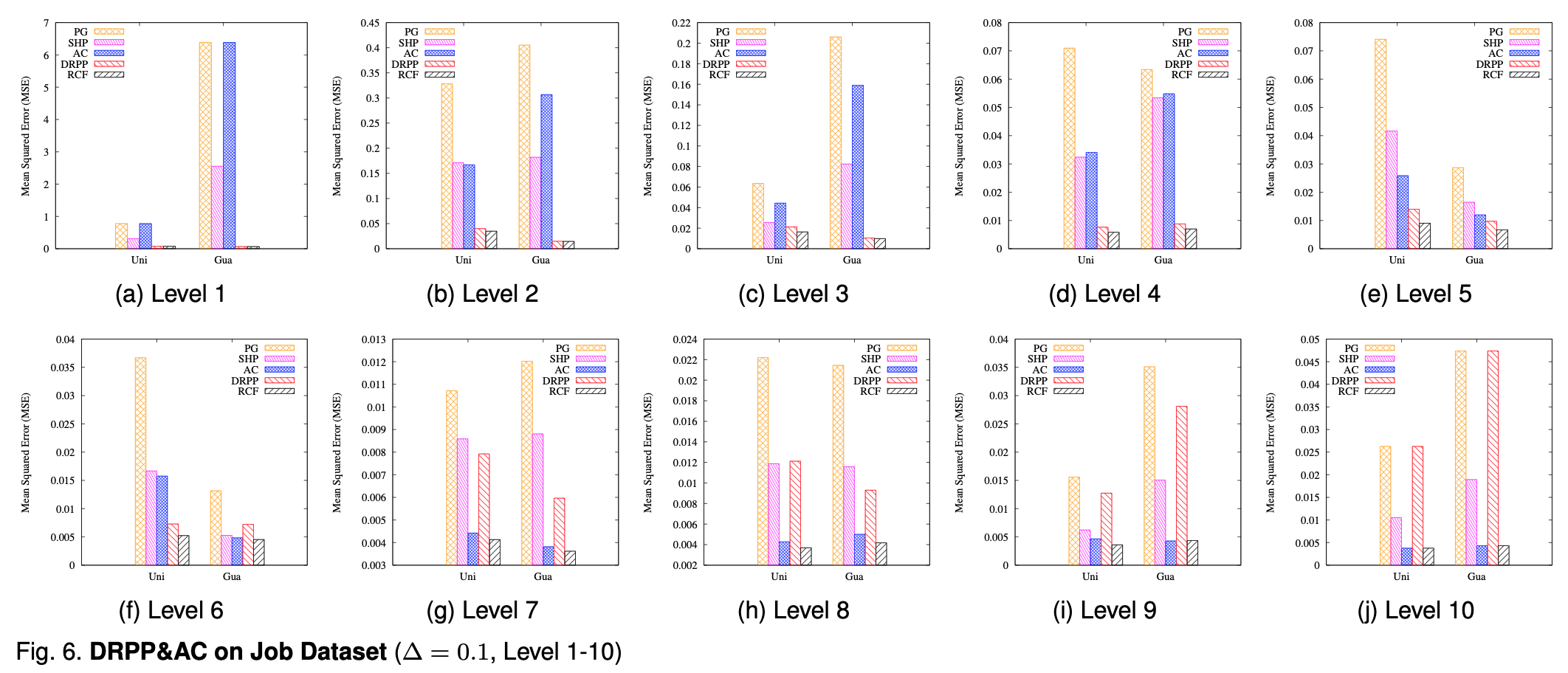
fig06

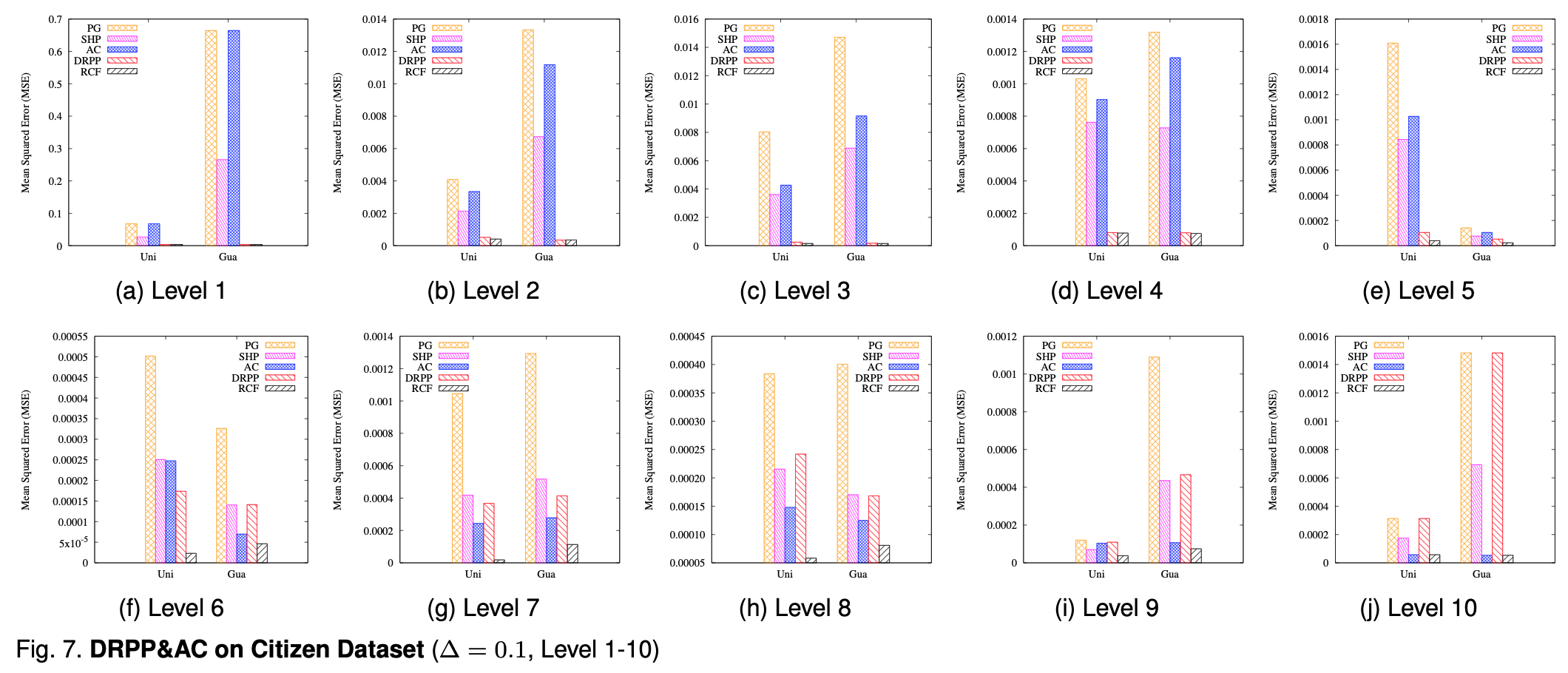
fig07

图6和图7展示了不同登记下不同方法的误差，可以看出来RCF还是比较厉害的。

也有一些其他的实验结果的分析，都是些锦上添花的工作，一方面我看的不是特别仔细，另一方面，我的表达也不一定合格，还是阅读原文更加准确。

个人总结

算法5倒是说了一种低等级数据变成高等级数据的方法，不过 Case 3实在花了我好长时间才大概搞懂了。按我的理解来说，完全可以避免 高等级+低等级->中等级 这种流程啊，只要低等级逐级生成高等级数据就好了，根据Post-Processing，这完全没问题。比如L4到L1，先从L4到L3，再从L3到L2，再从L2到L1，这样一轮，就不用再生成L3,L2了，暴力，简单，易懂，多好。

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》

Thanks for rewarding