论文阅读-Bidirectional Sampling for Handling Missing Data with Local Differential Privacy

发表于 | 更新于 | 分类于 | 阅读次数：

文章地址：BiSample: Bidirectional Sampling for Handling Missing Data with Local Differential Privacy
标题：BiSample: Bidirectional Sampling for Handling Missing Data with Local Differential Privacy
作者：Lin Sun, Xiaojun Ye, Jun Zhao, Chenhui Lu, Mengmeng Yang
发表会议：DASFAA 2020

  • Introduction
  • Preliminaries and Problem Definition
    • Local Differential Privacy (LDP)
    • Problem Definition
  • BiSample: Bidirectional Sampling Technique
  • Using BiSample for Missing Data Perturbation
  • Experiments
    • Experimental Settings
    • Varying User Behavior
    • Varying Missing Rate
    • Varying Size of Data
  • Conclusion

Introduction

随着大数据技术的发展，通常会收集和分析用户方的大量数据。在在线调查系统中，统计信息（尤其是频率和平均值）可以帮助调查人员了解整个调查人口。但是，收集用户数据存在隐私泄露的风险。LDP作为保护隐私数据收集和分析的解决方案，提供了可证明的隐私保护。通常，具有LDP保证的协议可以分解为Encode-Perturb-Aggregate范式。对于单轮数据共享，每个用户 encode 他的值（或元组）为特定的数据格式，然后 perturb 编码后的值以解决隐私问题。最后，所有受干扰的数据都由不受信任的收集器aggregated。带有LDP保证的机制已在许多现实世界的数据收集系统中实现，例如Google的RAPPOR和Microsoft的遥测数据分析系统。

尽管 LDP 可以平衡用户的隐私和数据有效性，但是现有解决方案假定被调查的用户真实地遵循收集过程。但是，在调查系统中，即使调查人员声称收集过程满足 LDP，出于以下考虑，个人仍可以拒绝提出一些具体问题：

  • 他们认为所提供的隐私保护级别很低

  • 有些用户只是不想告诉任何有关该问题的信息。

例如，如果研究人员设计了一种 3-LDP 机制来进行与个人相关的数据分析，那么那些认为隐私保护足够好的人将为他们提供真正的数据，而那些非常关心自己健康状况的人可能会回避诸如``您有癌症吗？’’之类的某些问题，因为他们认为LDP机制内置的隐私保护保证不够私密。由于现有的解决方案需要输入，因此这些人会随机选择一个答案（或仅回答“否”）并将其用于摄动（我们称这些 fake answers）。 fake answers答案将导致回避偏见。

在本文中，我们考虑了一种``提供空值’’方式来避免用户干扰数据时的虚假答案。 上图列出了用户的隐私偏好和每个调查问题的原始答案。 当提供的隐私保护级别未达到预期水平时，被调查用户不会发送虚假答案，而是发送空值以避免估计结果有偏差。 不受信任的聚合者想分析基本的统计信息，对于每个问题，1）多少人提供真实价值，2）整个调查人口的频率/平均值是多少。

本文首次考虑了用户合作对估计准确性的影响。 本文首先提出一种称为BiSample的双向采样机制，并将其用于数值微扰。 然后，将BiSample扩展为能够进行null-value perturbation，同时仍能实现LDP。 总的来说，本文提出以下贡献：

  • 第一次，我们认为并非所有用户都将在收集和分析框架中提供真正的数据以供扰动。我们建议的缺失数据扰动框架通过对用户的隐私保护偏好进行建模，从而为改进数据有效性提供了新见解。
  • 我们提出BiSample，一种用于数据扰动的双向采样机制。确切地说，BiSample机制可以代替Harmony解决方案进行均值估计。此外，我们将BiSample扩展为能够扰乱空值数据。我们的机制可以分析提供真实答案的用户的比率，并且可以将其用于具有LDP保证的频率/均值估计。
  • 由于建议的框架可用于估计在隐私预算$ \ epsilon $下提供真实价值的用户的比率，因此BiSample机制可用于研究聚合器如何适当地设置隐私预算。
  • 通过实验，所提出的机制比现有机制实现的估计误差更低。

Preliminaries and Problem Definition

LDP的背景介绍就忽略了，看一下本文研究的问题定义。首先，定义的符号如下所示：

用户隐私偏好的建模。如引言部分所述，对于一个调查问题，不同的用户具有不同的隐私首选项。 在不失一般性的前提下，我们使用$ \epsilon_u ^ i $来描述$ u_i $的隐私保护首选项，并且我们假设用户$ u_i $仅在提供的隐私保护级别高于预期水平时与数据收集器协作（ 这是$ \epsilon \le \epsilon_u ^ i $）。 当提供的隐私保护级别不符合预期时（$ \epsilon> \epsilon_u ^ i $），用户$ u_i $提供一个空值（由$ v_i = \bot $表示），而不是假的扰动答案 。扰动之后，聚合器从用户端收集数据，聚合器希望了解有关所有用户的一些统计信息，尤其是所有用户的空值率和均值。

缺失数据均值：对于一列数据 $\boldsymbol{v} = \{v_1, v_2, …, v_n\}$ 其中 $v_{i:i\in [n]}$ 来自用户 $u_i$ 并且范围为 $ [-1,1] \cup \{\bot\}$, 带有缺失数据的 $\boldsymbol{v}$ 的均值定义为:

当数据中不包含缺失数据时，缺失数据均值即等同于传统的均值。

BiSample：双向采样方法

在提出用于丢失数据扰动的解决方案之前，我们首先提出一种双向采样技术，称为\ textit {BiSample机制}。 BiSample机制将值$ v \in [-1，1] $作为输入，并输出一个扰动的元组$ \langle s，b \rangle $，其中$ s $代表采样方向，$ b $代表 $ v $。 具体来说，BiSample机制包含两个基本采样方向，定义为：

  • 负采样：负采样用于离散化后-1的比例，负采样的过程为：
  • 正采样：正采样用于离散化后1的比例，正采样的过程为：

假设输入域为$ [-1，1] $，Algorithm2显示BiSample的伪代码。 不失一般性，当输入域为$ [L，U] $时，用户可以（i）计算$ v’= \frac {2} {U-L} \cdot v + \frac {L + U} {L-U } $，（ii）使用BiSample机制扰乱$ v’$，（iii）共享$ \langle s，(\frac{U-L}{2} ）\cdot b + \frac{U+L}{2} \rangle $与聚合器，其中$ s $表示采样方法，$ b $是$ v’$的采样结果。 在Algorithm2中，第2-3行表示负采样过程，第5-6行表示正采样。 现在，我们证明正采样和负采样的组合满足$ \epsilon $ -LDP。

定理1：$\mathcal{M} = \operatorname{BiSample}(\cdot)$满足$\epsilon$-LDP

证明：对于输入 $t_1, t_2 \in [-1,1]$ 和输出 $o \in \operatorname{Range}(\mathcal{M})$，我们有：

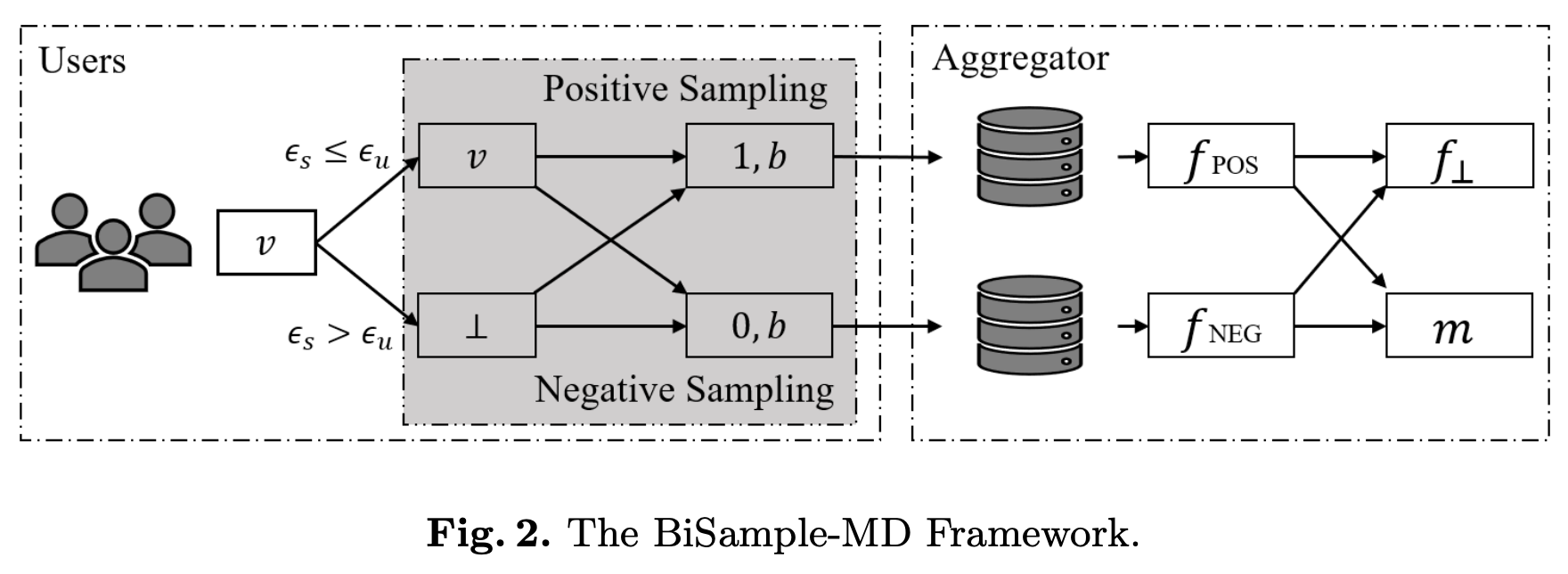
使用BiSample摄动，输入域中的值$ v_i $被摄动为两位元组$\mathcal{M}_{\operatorname{BiSample}}(v_i) = \langle s_i, b_i \rangle$。 结果是双重含义的。 首先，$ s_i $指示采样机制是否为正采样。 其次，$ b_i $代表具有相应采样机制的采样值。 对于聚合器，令$ \mathcal {R} = \{\langle s_1，b_1 \rangle，\langle s_2，b_2 \rangle，… \langle s_n，b_n \rangle \} $是从所有接收到的扰动数据 用户和$f_{\operatorname{POS}}$（分别为$ f _ {\operatorname {NEG}} $）是正采样（负采样）的合计频率，由下式给出：

接下来，我们证明君之估计的结果是无偏的

本篇内容到这里就结束了，欢迎关注公众号《差分隐私》，获取更多前沿技术。

《差分隐私》

Thanks for rewarding