The Problem of Overfitting

目前已经了解了线性回归和逻辑回归，可以解决很多问了，当时当这些东西应用到实际的应用中，会遇到过拟合的问题（overfitting）这会导致实际的效果很差。

本小姐解释什么是过拟合以及接下来几节讲解通过正则化（Regularization）来改善和减少过拟合问题。

以之前的房价预测为例，如果我们有非常多的特征，我们可以通过学习，几乎可以将代价函数降到0，但是这样就不能推广到新的数据。

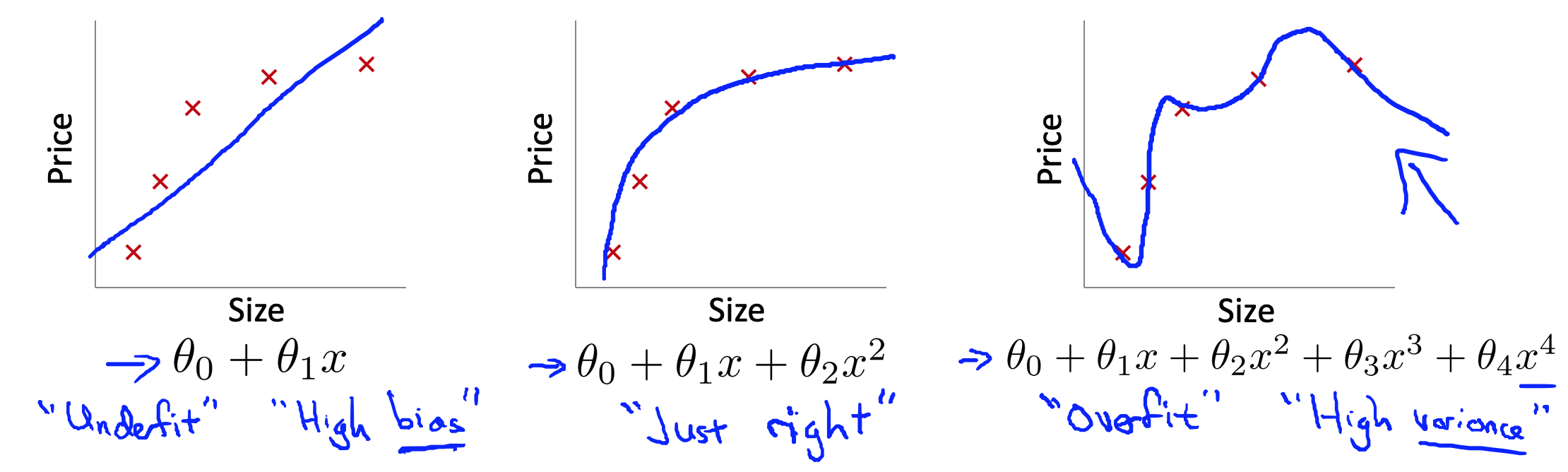
第一个模型是线性模型，他是欠拟合（underfitting）的，不能很好地适应训练数据。第三个模型是一个四次方模型，过于强调拟合原始数据，对于原始数据可以使得代价函数降到0，但是对于新的数据的预测效果将会比较差，这是过拟合的（overfitting）。中间的模型最合适。

在分类的过程中，也会遇到过拟合的情况，如：

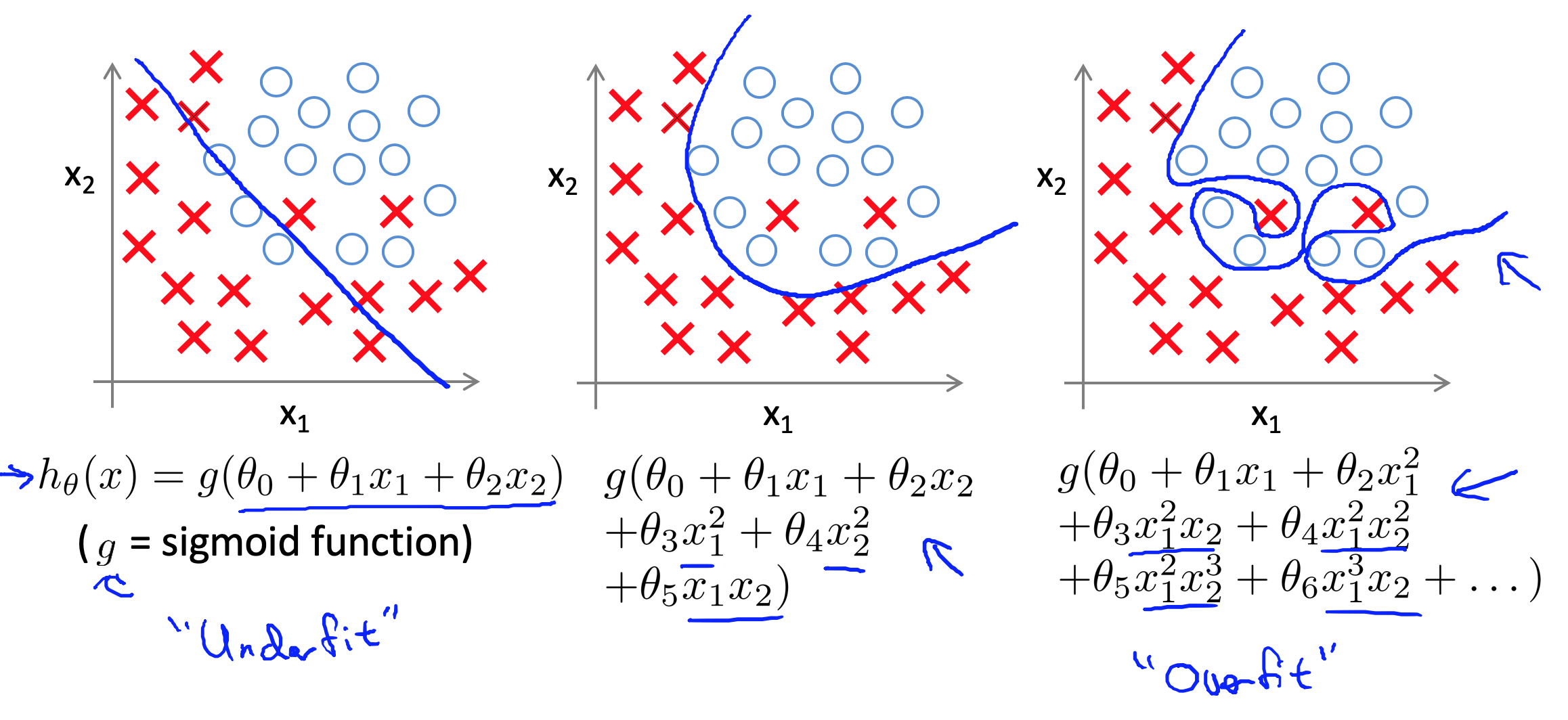
很显然，我们希望我们的模型是中间的情况。那么如果发现了过拟合，该如何处理？

可以丢掉一些我们不需要的特征，比如去掉高次项。我们可以手工选择保留那些特征，或者用算法帮忙，如 PCA。
正则化。保留所有的特征，但是减少参数的大小（magnitude）。

Cost Function

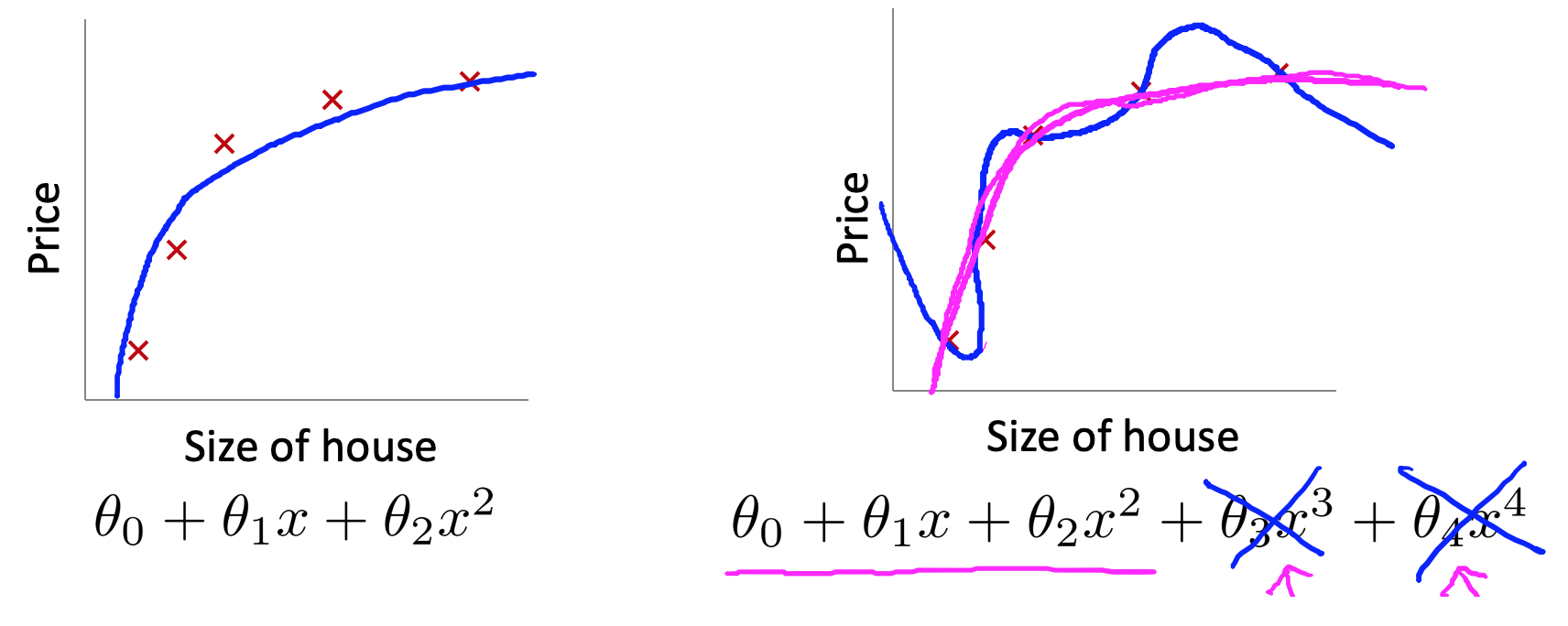
回到这个案例，如果我们使用的模型是 ${h_\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}^2}+{\theta_{3}}{x_{3}^3}+{\theta_{4}}{x_{4}^4}$，那么就会出现过拟合。上面提到的一种解决方法就是把三次项和四次项去掉，这样就可以解决过拟合的问题。从另一个角度思考这个问题，去掉高次项主要是使得 ${\theta_{3}}{x_{3}^3}+{\theta_{4}}{x_{4}^4}$ 可以尽可能地小。那么我们可以在代价函数中对 $\theta_3,\theta_4$ 加一个惩罚项，这样优化的目标就变成了：

$\min _{\theta} \frac{1}{2 m}\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+1000 \cdot \theta_{3}^{2}+10000 \cdot \theta_{4}^{2}\right]$

这样在优化的过程中，为了使得代价函数尽可能地小，$\theta_3,\theta_4$ 的值就会尽可能小。

加入我们有非常多的特征，我们其实是并不知道哪些项是需要进行惩罚的，我们通常的组佛啊是对所有的特征进行惩罚，让代价函数自动去学习这些惩罚的程度，这样我们就能得到一个较为简单的防止过拟合问题的假设：

$J(\theta)=\frac{1}{2 m}\cdot\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$

其中，$\lambda$ 被称为正则化参数（Regularization Parameter）。注意，我们一般不对 $\theta_0$进行惩罚。这样我们就能学习到这样的回归模型：

很显然，增加的惩罚项可以使得对应的 $\theta$ 尽可能小，那么 $\lambda$ 改怎么取比较好呢？

如果取得太大了，所有的 $\theta$（不包括 $\theta_0$）都会取景于0，这样会得到一条近似平行于 $x$ 轴的直线，
设置的太小了，依然会存在过拟合问题。

Regularized Linear Regression

这里我们将正则化用在之前的线性回归中。之前我们用两种方法解决了线性回归的问题，梯度下降和正规方程。最优化的目标为：

$J(\theta)=\frac{1}{2 m}\cdot\left[\sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}+\lambda \sum_{j=1}^{n} \theta_{j}^{2}\right]$

Regularized Descent

梯度下降，实际上就是要去计算梯度，可以直接给出梯度为：

$\begin{cases} \theta_{0}=\theta_{0}-a \frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)}\right)\\ \theta_{j:j\in[1,n]}=\theta_{j}-a\left[\frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}+\frac{\lambda}{m} \theta_{j}\right]\right. \end{cases}$

在第二个式子中，我们可以做如下变化：

$\theta_{j}:=\theta_{j}\left(1-a \frac{\lambda}{m}\right)-a \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}$

正则化线性回归的梯度下降算法的变化在于，每次都在原有算法更新规则的基础上令 $\theta $ 值进行一个放缩。

Regularized Normal Equation

我们同样也可以利用正规方程来求解正则化线性回归模型，结果为：

$\theta=\left(X^{T} X+\lambda\left[\begin{array}{ccccc}0 \\ & 1 \\ & & 1 \\ & & & \ddots \\ & & & & 1\end{array}\right]\right)^{-1} X^{T} y$

其中，矩阵的大小为 $(n+1)\times(n+1)$。有趣的是，加上了这个矩阵之后，左边括号里面的矩阵是一定可逆的。

Regularized Logistic Regression

在逻辑回归中，增加一个惩罚项之后，代价函数变为：

$J(\theta)=\frac{1}{m} \sum_{i=1}^{m}\left[-y^{(i)} \log \left(h_{\theta}\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right) \log \left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]+\frac{\lambda}{2 m} \sum_{j=1}^{n} \theta_{j}^{2}$

所以我们计算出这个代价函数的梯度即可，为：

$\begin{cases} \theta_{0}=\theta_{0}-a \frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{0}^{(i)}\right)\\ \theta_{j:j\in[1,n]}=\theta_{j}-a\left[\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) x_{j}^{(i)}+\frac{\lambda}{m} \theta_{j}\right] \end{cases}$

依然，这个梯度和线性回归的梯度看上去是一样的，但是本质不同。