本章节讲解神经网络，组织结构如下：

Neural Networks: Representation
- Non-linear Hypotheses
- Neurons and the Brain
- Model Representation I
- Model Representation II
- Examples and Intuitions I
- Examples and Intuitions II
- Multiclass Classification

Non-linear Hypotheses

之前提到的一点是当特征非常多时，计算的负荷会非常大，比如：

上面的例子中，当我们使用 $x_1,x_2$ 的多项式组合进行预测时，可以得到较好的结果。当我们有非常多的特征的时候，比如我们有100个变量，如果采用两两特征组合的方式，那么这100个特征会构成这样一个多项式 $(x_1x_2+x_1x_3+x_1x_4+…+x_2x_3+x_2x_4+…+x_{99}x_{100})$，这回产生5000个新的特征，对于逻辑回归来说，需要计算的特征太多了。

扑通的逻辑回归模型是不能高效地处理这么多的特征的，这时候我们就需要用到神经网络。

Neurons and the Brain

这一小的章节科普神经元和大脑的相关知识，就跳过了。

Model Representation I

为了创建神经网络模型，我们一般现需要大脑中的神经网络是如何工作的。

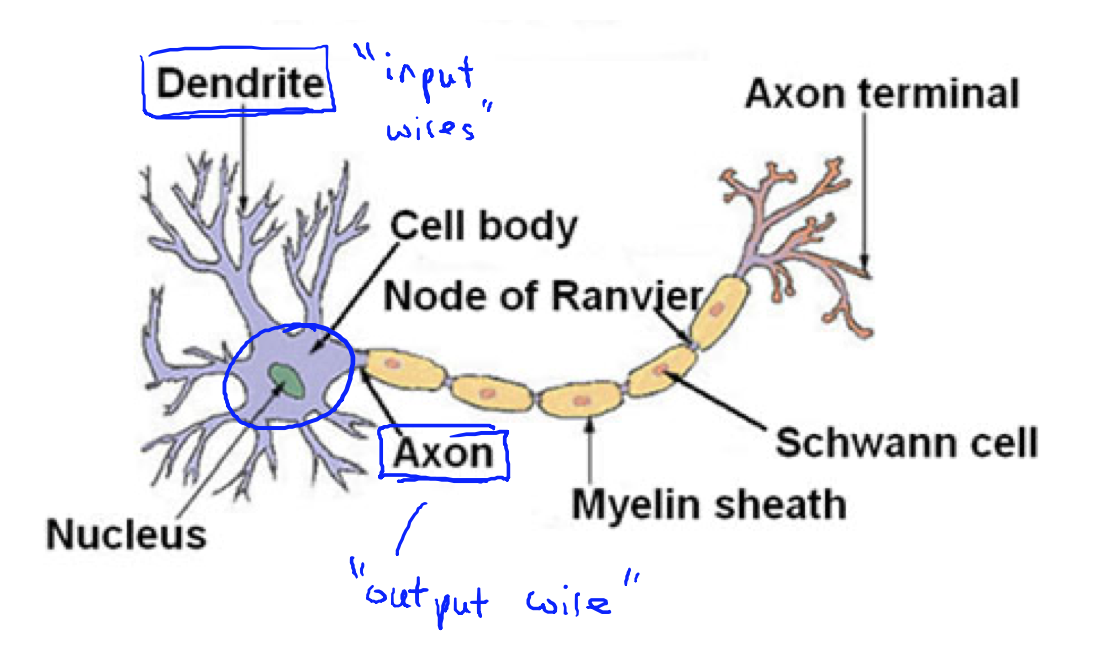
大脑中，每一个神经元可以认为是一个处理单元，或者神经核（processing unit/ nucleus），其含有诸多输入/树突（input/Dendrite），并且有一个输出/轴突（output/Axon）。输出连接下一个神经元作为下一个神经元的输入。有了大量的神经元，就有了神经网络。

一个神经元也叫做一个激活单元（activation unit），其才拿一些特征作为输入，并且产生一个输出。比如下图就是一个神经元：

多个神经元组合而成的神经网络，效果如下：

其中 $x_1,x_2,x_3$ 是输入单元（Input Units），$a_1,a_2,a_3$ 是中间单元，负责处理之后向下传递信息，最后是输出单元，负责计算 $h_\theta(x)$。我们也会按层对神经网络进行切分，上图的是一个三层的神经网络，第一层为输入层（Input Layer），最后一层为输出层（Output Layer），中间的都叫隐藏层（Hidden Layers），此外，每层都包含一个偏置（Bias Unit）。

在本节中，我们采用上述的记法，$a_{i}^{\left( j \right)}$ 代表第$j$ 层的第 $i$ 个激活单元。${\theta }^{\left( j \right)}$代表从第 $j$ 层映射到第$ j+1$ 层时的权重的矩阵，例如${\theta }^{\left( 1 \right)}$代表从第一层映射到第二层的权重的矩阵。其尺寸为：以第 $j+1$层的激活单元数量为行数，以第 $j$ 层的激活单元数加一为列数的矩阵。例如：上图所示的神经网络中${\theta }^{\left( 1 \right)}$的尺寸为 3*4。

那么对应上图，激活单元和输出分别为：

$\begin{array}{l}a_{1}^{(2)}=g\left(\Theta_{10}^{(1)} x_{0}+\Theta_{11}^{(1)} x_{1}+\Theta_{12}^{(1)} x_{2}+\Theta_{13}^{(1)} x_{3}\right) \\ a_{2}^{(2)}=g\left(\Theta_{20}^{(1)} x_{0}+\Theta_{21}^{(1)} x_{1}+\Theta_{22}^{(1)} x_{2}+\Theta_{23}^{(1)} x_{3}\right) \\ a_{3}^{(2)}=g\left(\Theta_{30}^{(1)} x_{0}+\Theta_{31}^{(1)} x_{1}+\Theta_{32}^{(1)} x_{2}+\Theta_{33}^{(1)} x_{3}\right) \\ h_{\Theta}(x)=g\left(\Theta_{10}^{(2)} a_{0}^{(2)}+\Theta_{11}^{(2)} a_{1}^{(2)}+\Theta_{12}^{(2)} a_{2}^{(2)}+\Theta_{13}^{(2)} a_{3}^{(2)}\right)\end{array}$

如果在第 $j$ 层有 $s_j$ 个神经元，第 $j+1$ 层有 $s_{j+1}$ 个神经元，那么 $\Theta^{(j)}$ 的维度就是 $s_{j+1} \times\left(s_{j}+1\right)$。这是因为还有一个偏置，或者说还有一个1的常数项输入 $x_0$。

由于每一个 $a$ 都是由上一层的 $x$ 和 $\Theta$ 得到的，我们把这样的从左到右的算法称为前向传播算法（Forward Propagation）。

Model Representation II

Examples and Intuitions I

Examples and Intuitions II

Multiclass Classification

和之前的逻辑回归类似，我们也会碰到多元分类问题，在神经网络中，我们依然采用的是 One-vs-All 策略。

假设数据是：$\left(x^{(1)}, y^{(1)}\right),\left(x^{(2)}, y^{(2)}\right), \ldots,\left(x^{(m)}, y^{(m)}\right)$，我么需要对 $y$ 进行一个变化，使得其属于以下之一：

$\left[\begin{array}{l}1 \\ 0 \\ 0 \\ 0\end{array}\right], \quad\left[\begin{array}{l}0 \\ 1 \\ 0 \\ 0\end{array}\right], \quad\left[\begin{array}{l}0 \\ 0 \\ 1 \\ 0\end{array}\right], \quad\left[\begin{array}{l}0 \\ 0 \\ 0 \\ 1\end{array}\right]$

这样我们就可以解决多元分类的问题了，至于如何训练，下节揭晓。