吴恩达机器学习课程(14)-Dimensionality Reduction

发表于 | 更新于 | 分类于 ， | 阅读次数：

本章主要结构如下：

  • Motivation I: Data Compression
  • Motivation II: Visualization
  • Principal Component Analysis Problem Formulation
  • Principal Component Analysis Algorithm
  • Choosing The Number Of Principal Components
  • Reconstruction from Compressed Representation
  • Advice for Applying PCA

Motivation I: Data Compression

我们开始谈论第二种类型的无监督学习问题，称为降维。降维具体是什么就不解释了，可以看一个从三维到二维的降维的例子：

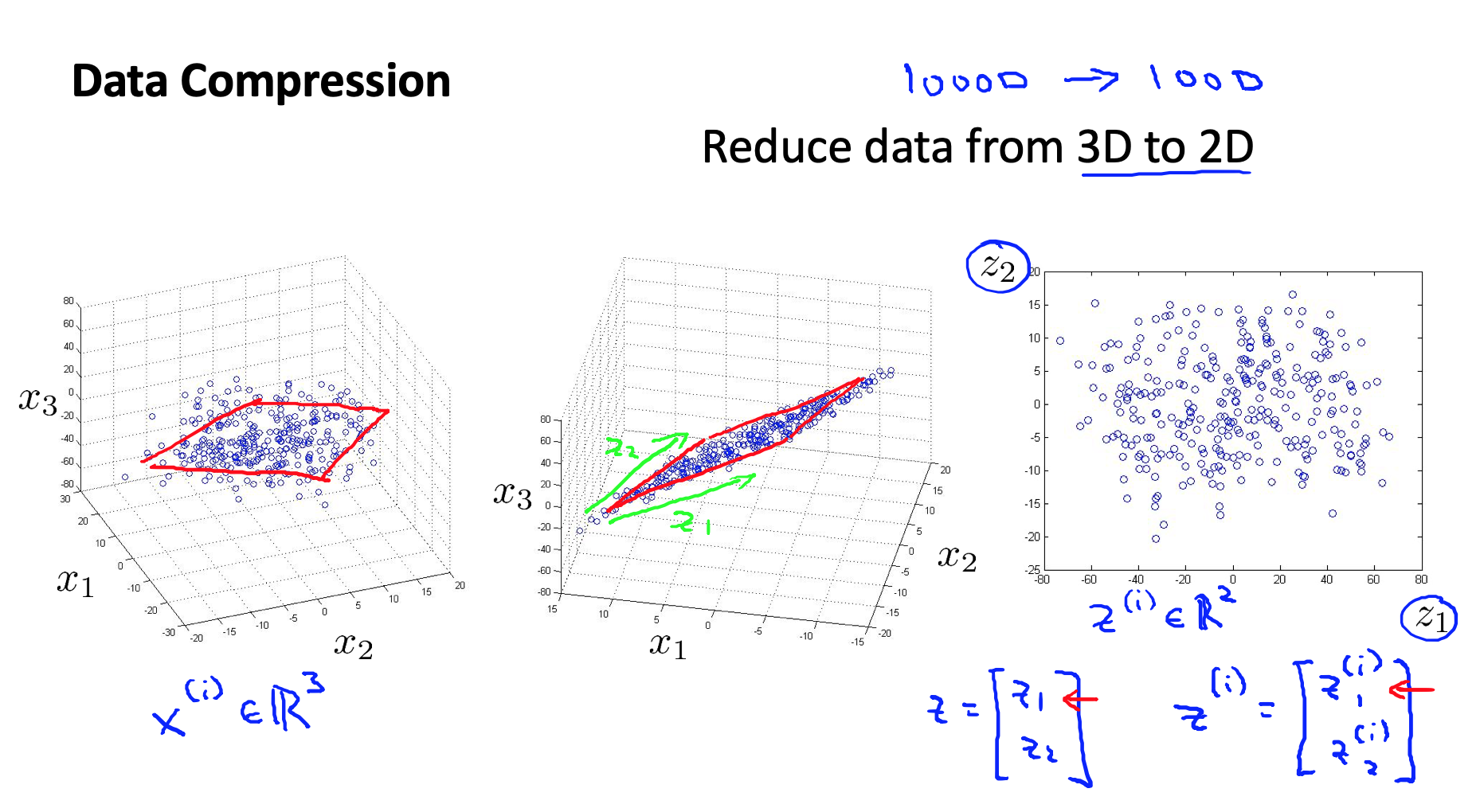
image-20200604215918101

Motivation II: Visualization

在许多及其学习问题中，如果我们能将数据可视化，我们便能寻找到一个更好的解决方案，降维可以帮助我们。

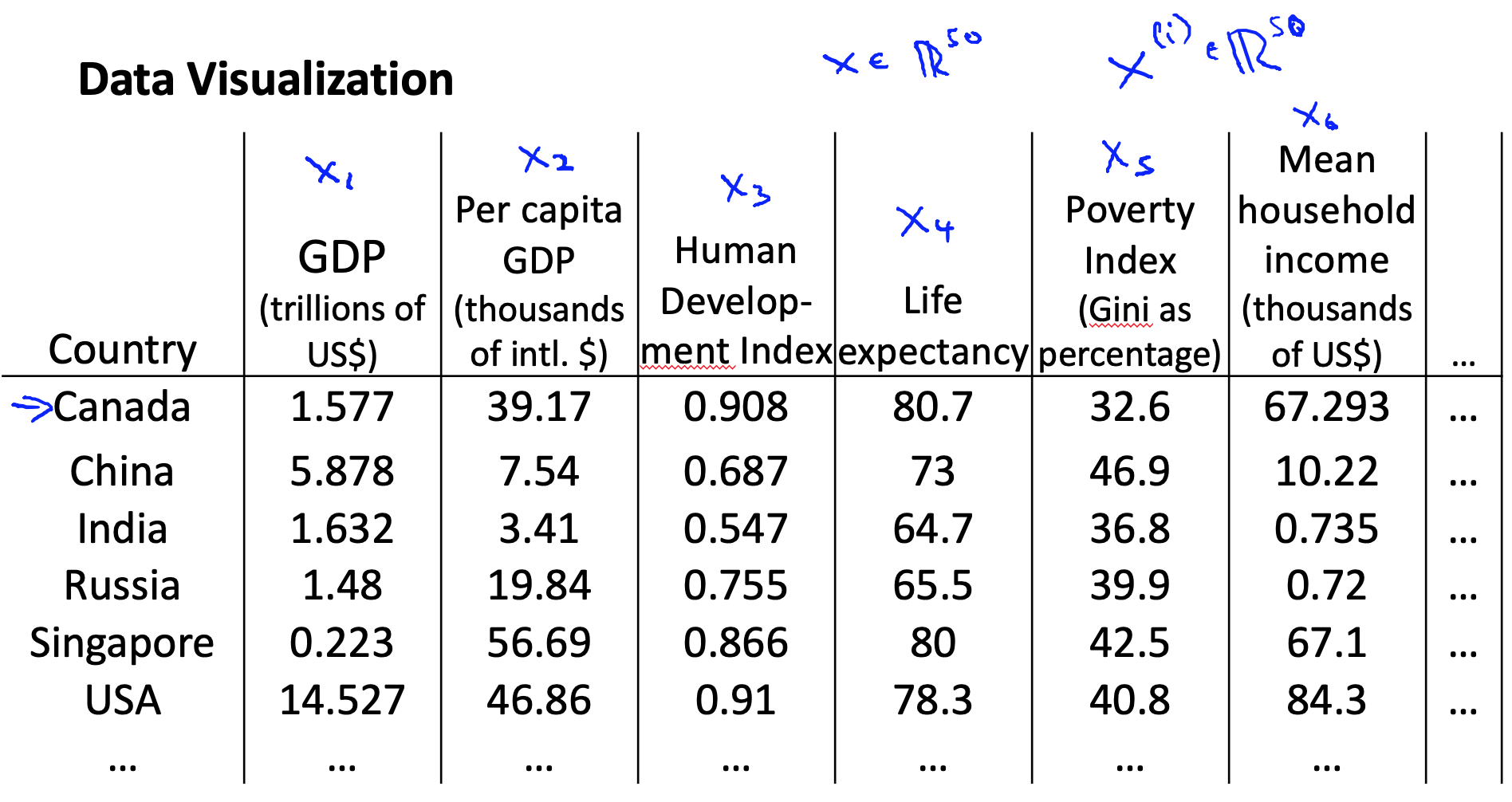
image-20200604220110191

假使我们有有关于许多不同国家的数据，每一个特征向量都有50个特征（如GDP，人均GDP，平均寿命等）。如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至2维，我们便可以将其可视化了。

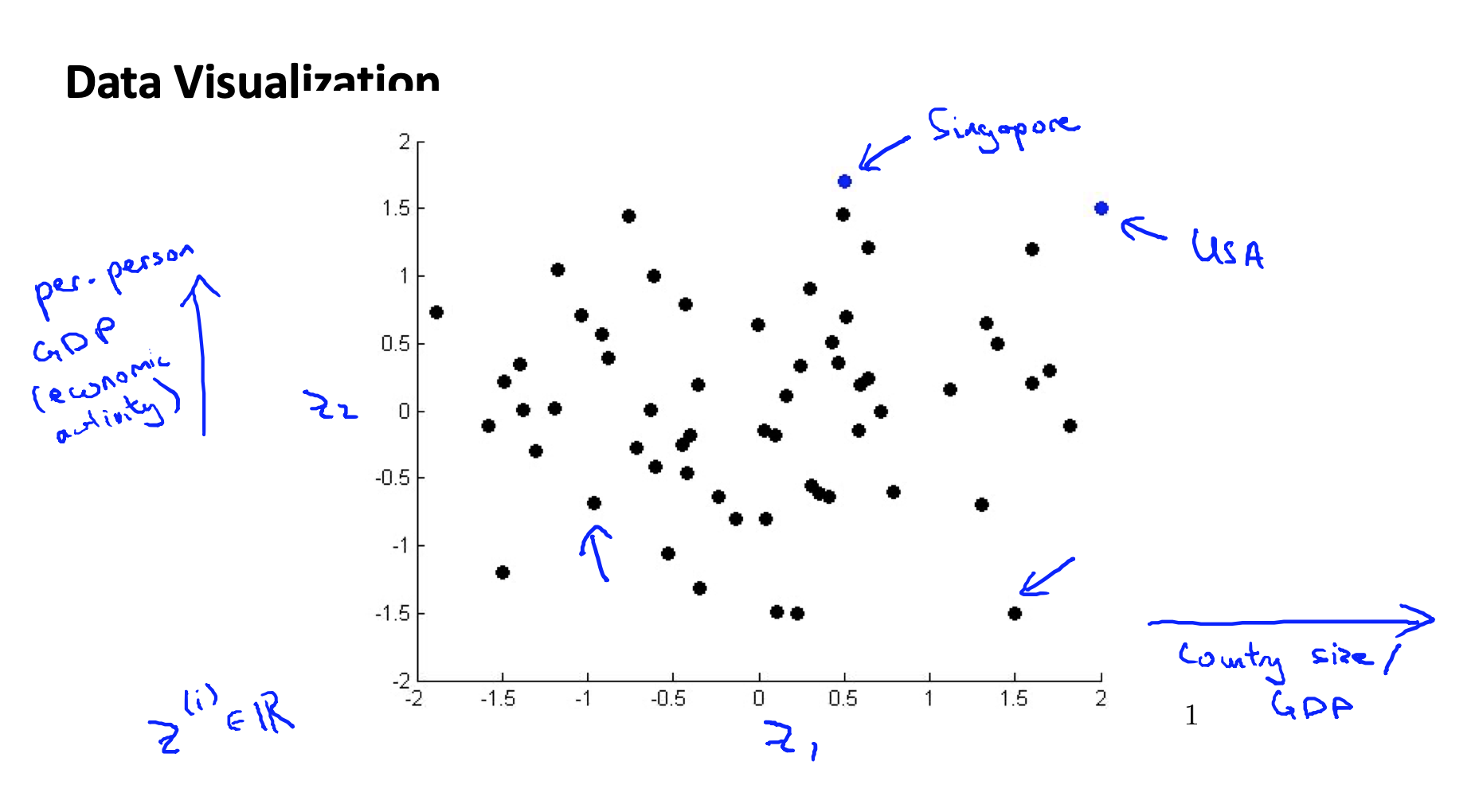
image-20200604220151824

这样，降维之后，可能横轴代表国家 GDP 的大小，然后纵轴代表人均 GDP ，比如美国可能在右上角，然后中国在右下角这样子。通过降维，我们可以更好地对数据进行可视化。

Principal Component Analysis Problem Formulation

主成分分析(PCA)是最常见的降维算法。

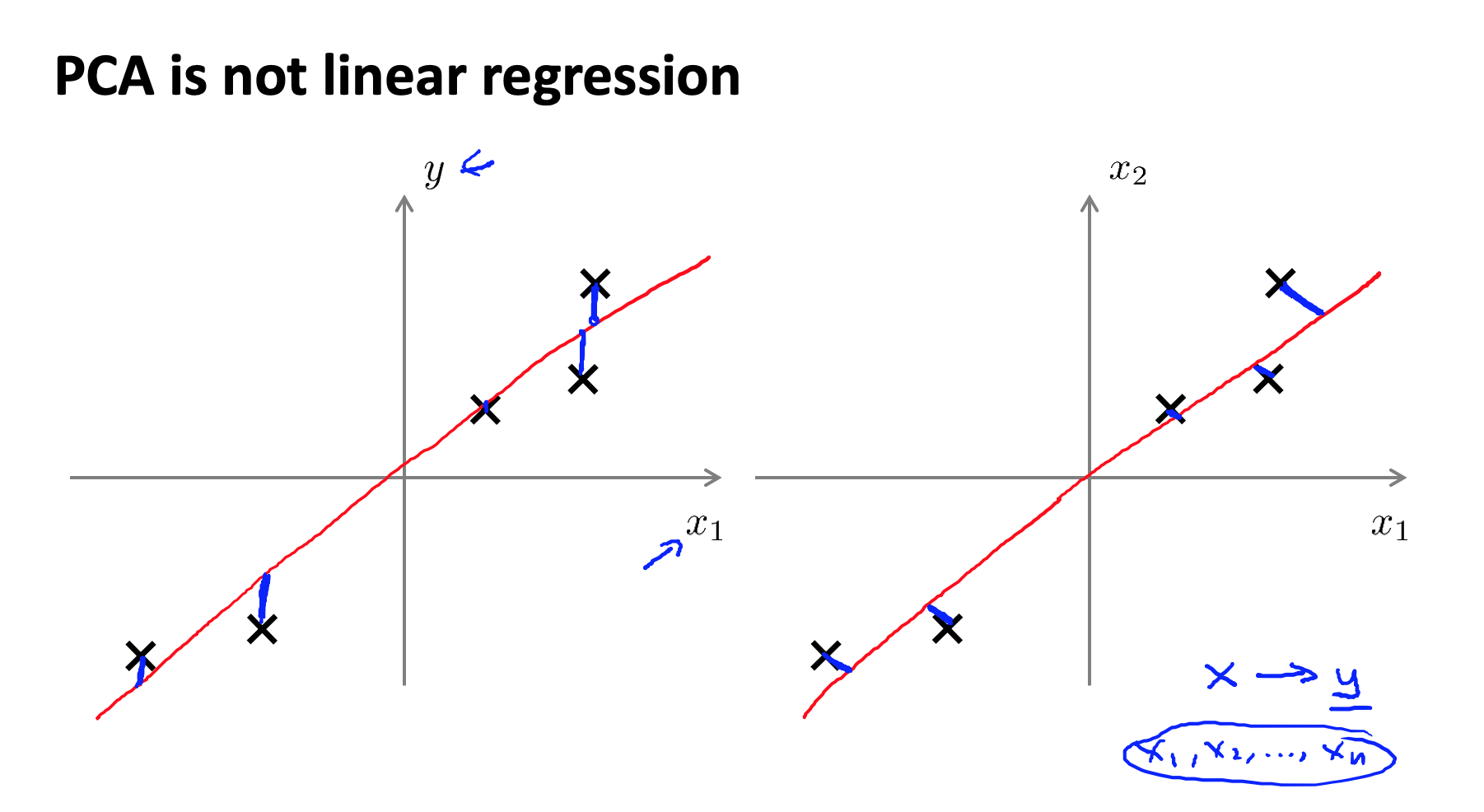
在PCA中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

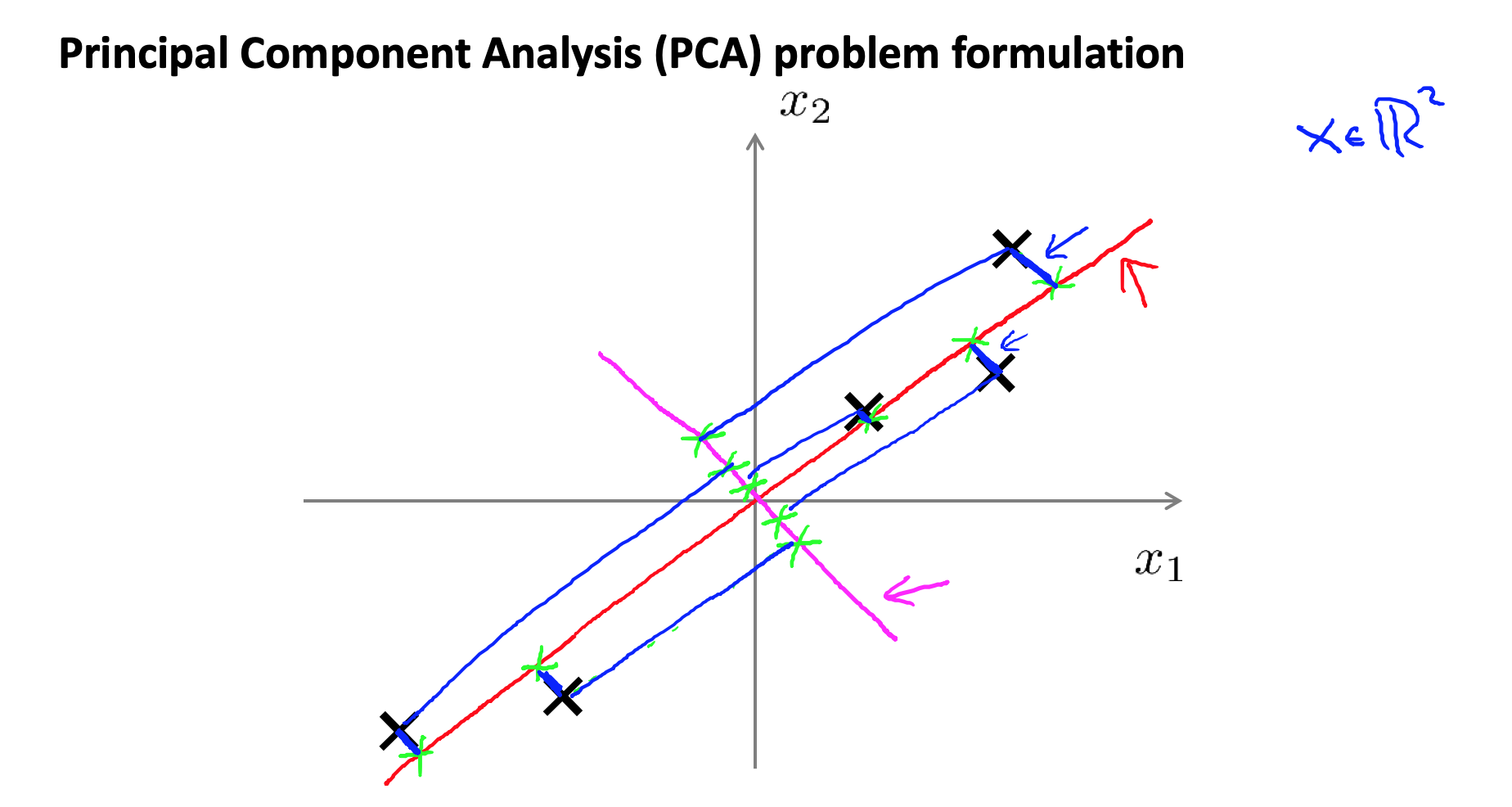
image-20200604220404956

在上图中，很显然，降到红色那条线比降维到粉红色那条线效果要更好。值得注意的是，PCA 和线性回归是不同的东西：

image-20200604220458884

PCA将$n$个特征降维到$k$个，可以用来进行数据压缩，如果100维的向量最后可以用10维来表示，那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后，还要保证数据的特性损失最小。

PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

PCA技术的一个很大的优点是，它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数或是根据任何经验模型对计算进行干预，最后的结果只与数据相关，与用户是独立的。

但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

Principal Component Analysis Algorithm

首先和其他的算法一样，先需要对数据进行预处理。

image-20200604220518608

在降维的过程中，需要这么几步：

  • 第一步是均值归一化。我们需要计算出所有特征的均值，然后令 $x_j= x_j-μ_j$。如果特征是在不同的数量级上，我们还需要将其除以标准差 $σ^2$。

  • 第二步是计算协方差矩阵（covariance matrix）$Σ$：

  • 第三步是计算协方差矩阵 $Σ$ 的特征向量（eigenvectors）:即SVD分解。在 Octave 里我们可以利用奇异值分解（singular value decomposition）来求解，[U, S, V]= svd(sigma)。

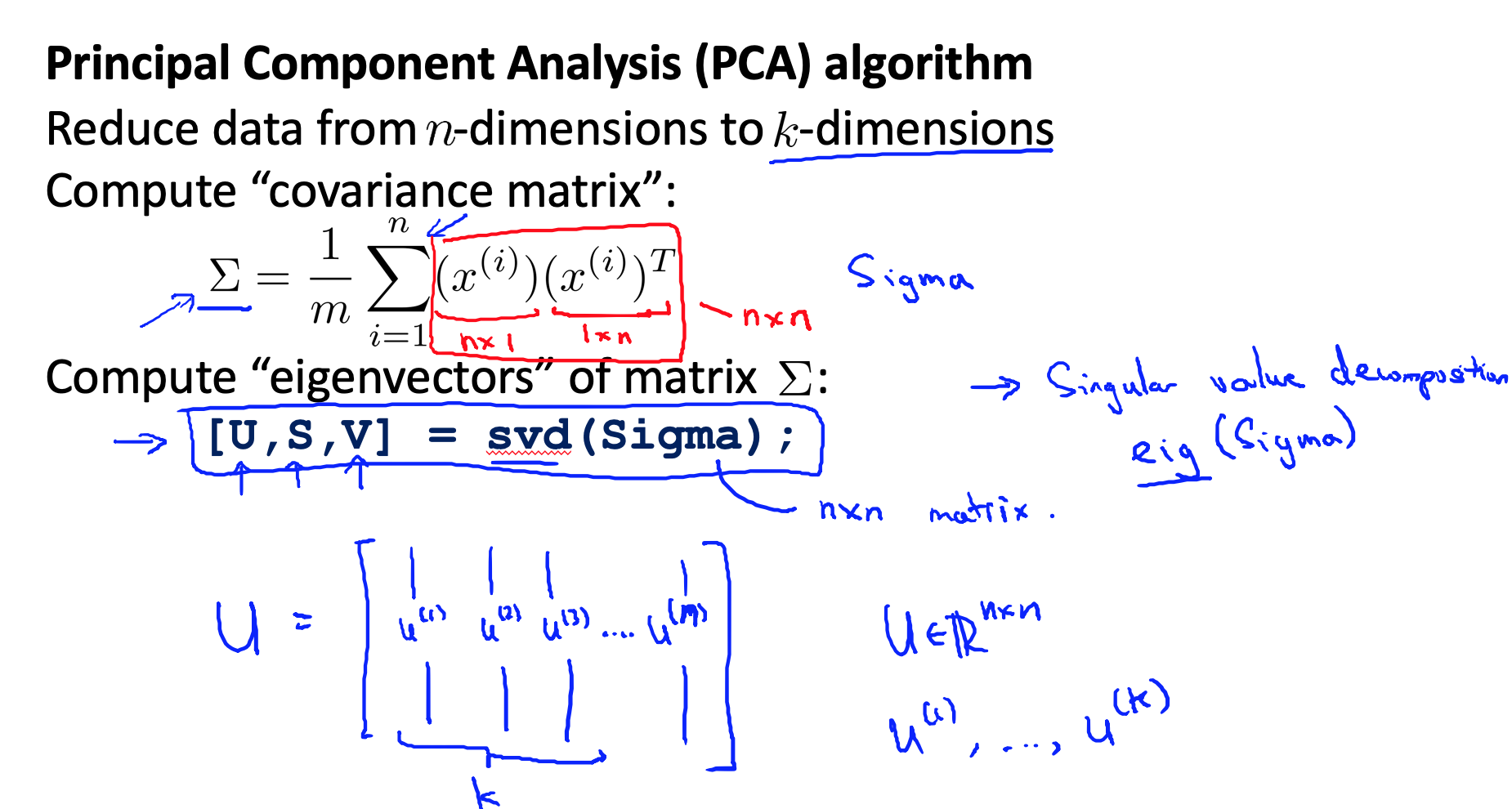
image-20200604220739238

经过SVD分解之后，我们就得到了这个 $U$。我们只需要从$U$中选取前$k$个向量，获得一个 $n×k$ 维度的矩阵，我们用 $U_{reduce}$ 表示，然后通过如下计算获得要求的新特征向量$z^{(i)}$:

其中 $x$ 是 $n×1$ 维的，因此结果为 $k×1$ 维度。注，我们不对方差特征进行处理。

Choosing The Number Of Principal Components

主要成分分析是减少投射的平均均方误差。训练集的方差为：$\dfrac {1}{m}\sum^{m}_{i=1}\left| x^{\left( i\right) }\right| ^{2}$，我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的$k$值。

如果我们希望这个比例小于1%，就意味着原本数据的偏差有99%都保留下来了，如果我们选择保留95%的偏差，便能非常显著地降低模型中特征的维度了。

我们可以先令$k=1$，然后进行主要成分分析，获得$U_{reduce}$和$z$，然后计算比例是否小于1%。如果不是的话再令$k=2$，如此类推，直到找到可以使得比例小于1%的最小$k$ 值（原因是各个特征之间通常情况存在某种相关性）。

还有一些更好的方式来选择$k$，当我们在Octave中调用“svd”函数的时候，我们获得三个参数：[U, S, V] = svd(sigma)。

image-20200604221634058

其中的 $S$ 是一个 $n×n$ 的矩阵，只有对角线上有值，而其它单元都是0，我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例：

也就是：

在压缩过数据后，我们可以采用如下方法来近似地获得原有的特征：

Advice for Applying PCA

假使我们正在针对一张 100×100像素的图片进行某个计算机视觉的机器学习，即总共有10000 个特征。

  • 第一步是运用主要成分分析将数据压缩至1000个特征
  • 然后对训练集运行学习算法
  • 在预测时，采用之前学习而来的$U_{reduce}$将输入的特征$x$转换成特征向量$z$，然后再进行预测

注：如果我们有交叉验证集合测试集，也采用对训练集学习而来的$U_{reduce}$。

错误的主要成分分析情况：一个常见错误使用主要成分分析的情况是，将其用于减少过拟合（减少了特征的数量）。这样做非常不好，不如尝试正则化处理。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。然而当我们进行正则化处理时，会考虑到结果变量，不会丢掉重要的数据。

另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。

Thanks for rewarding