标题&地址:TGM: A Generative Mechanism for Publishing Trajectories with Differential Privacy
作者:Ghane, Soheila, Lars Kulik, and Kotagiri Ramamohanarao
发表于:IEEE Internet of Things Journal
这篇论文提出了一种能够保证 $\epsilon$-differential privacy 的轨迹生成机制TGM。TGM包括两个阶段,他们首先运用图像生成算法来对数据进行编码并能准确地捕捉到运动目标轨迹的统计数据,之后TGM通过加噪来秘密地生成合成轨迹。个人认为本文提出的对 privacy budget 的分配算法是非常值得学习的,并且TGM首次提出了将静态或相对稳定的位置也考虑到生成轨迹中的想法。通过这篇论文的实验结果可知,TGM在减少内存需求的同时,能够实现较高的运算效率和数据可用性。
Mechanism Overview
TGM是一个包括两个阶段的轨迹隐私保护机制如算法1所示,步骤1用一个图解模型来编码使得每条轨迹是一串位置的经纬度坐标,TGM中的加噪过程在步骤二实现以满足 $\epsilon$-differential privacy。

阶段一:真实轨迹建模
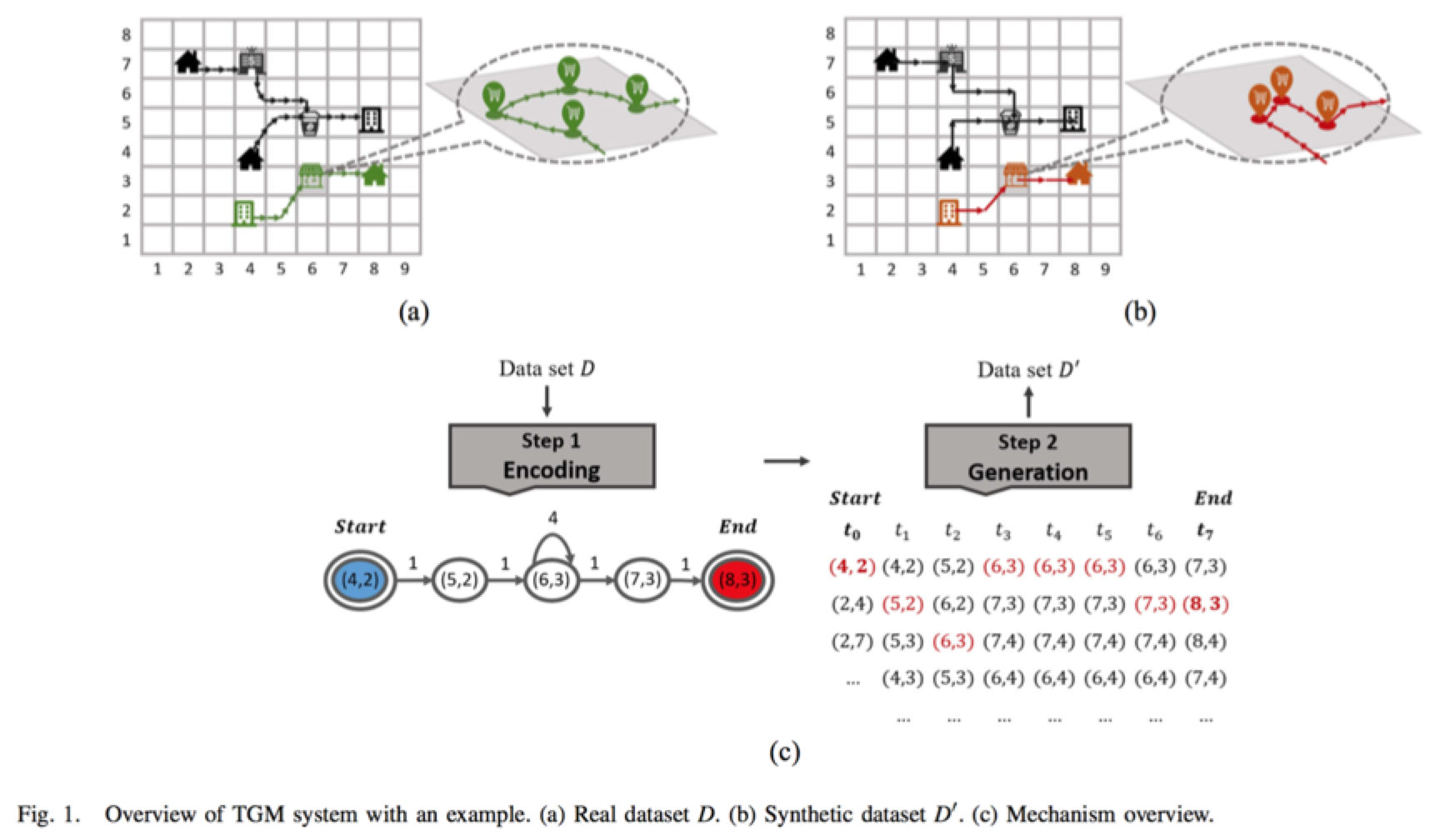
图1举例说明了TGM的过程,为了捕捉轨迹中的任一次运动行为,这篇论文提出了一个图像生成概率模型来准确地对给定轨迹进行建模。一个运动中的目标在每个时间节点或许运动到新的位置,亦或许保持在原地不动。本文的模型适合满足马尔可夫过程的轨迹,即基于近期的轨迹上的访问地点可以预测下一位置。在图1.(a)中画出了数据集D对应的真实轨迹,气泡对话框内展示的是用户在购物中心逗留的情况。图1.(c)中Encoding模块,每个节点表示的是图1.(a)中的网格单元,相邻两节点间的方向箭头表示目标从一个节点移动到另一个节点,蓝色椭圆和红色椭圆分别表示轨迹的起点和终点,这样便把一个轨迹编码为一个网络结构图。
阶段二:生成合成轨迹
有了图解模型G之后,第二步就是生成合成的轨迹。本文提出了一个原创算法在生成轨迹的过程中适应性地增加噪声,随机化这个过程使得这个算法能用任意长度来维持运动轨迹的模式。本文同时使用了指数机制(EM)和拉普拉斯机制(LM),给定生成轨迹的一些已知的位置信息,可以计算下一步的转移概率:移动到下一个相邻位置的概率、保持在同一位置的概率和是轨迹终点的概率,之后便可用EM来选择一个点,用LM来加噪声。这时需要分配总体的隐私预算,为EM的隐私预算,为LM的隐私预算。生成轨迹的过程将在到达终点或隐私预算被完全消耗的时候停止。图2.(b)为生成数据集D’对应的轨迹图像,图1.(c)中步骤二Generation模块的数据表展示了生成一个轨迹的过程。
Preliminaries
轨迹数据集
一条轨迹通常表示为 $\mathrm{T}=\left\{\left(s_{1}, t_{1}\right), \ldots,\left(s_{n}, t_{n}\right)\right\}$,其中$s_i$表示一个位置坐标,$t_i$表示一个时间戳。在连续时间内,一段轨迹上的点都是重复的表示这个运动目标静止在某一位置上,因此本文给出了轨迹片段的定义:

图像生成模型
算法2用非平凡拓扑时空图来对轨迹进行建模,模型表示一个定向图,分别为节点和边的集合。在空间上,每个节点有八个相邻的网格单元,所以每个节点的出度为9(包括一个自我转移)。在每个时间点,可以用k阶马尔可夫链来预测轨迹的状态,k值随着时间而增加。图形结构使我们能够建模任意长度轨迹的序列和分布并且区分出静态和动态的轨迹片段,同时捕捉到轨迹间的交互链接模式。

Private Model Learning
在一个轨迹生成过程中,有以下三部分需要学习:起始位置的可用性、转移概率和终止状态,这些内容可以由图像模型中的计数情况得到。算法3所示的轨迹生成过程能确保端到端的隐私保护从轨迹的起点到终点,并且能动态调整每一步中可导致不同轨迹长度的隐私预算。轨迹生成过程由确定初始点开始并持续选择接下来的位置,函数First()和Next()用于计算可能的初始位置和下一位置的效用,此时EM用于随机挑选一个潜在的位置来确保隐私的保护。函数DirChng()用于计算方向的变化,如果方向的变化小于偏差阈值,表示运动方向没有很大程度上地改变,这时下一位置为函数EstLoc()的结果并且相应的EM的隐私预算将被归还用于之后的步骤中,否则将会用EM来选择位置。函数Rtn()用一个适应性的预算分配方法来分配$\epsilon’$。

隐私预算分配
如果生成轨迹的长度为n,总共的 $\epsilon$ 将在 n 步中被分割,然而 n 值是未知的因为生成轨迹过程能够在任一步终止。因此本文提出一个战略来基于敏感度适应性地对每一步分配隐私预算,假设最多的隐私预算将会分配给第一个点并且在之后的步骤中序列性地降低分配到的预算,即$\varepsilon_{i+1}^{\prime}<\varepsilon_{i}^{\prime}$。设定一个临界值$\eta=10^{-4}$,当$\varepsilon_{i}^{\prime} \leq \eta$时,终止生成轨迹的过程。由于会对生成轨迹的长度产生一个上限,引入一个预算归还方法来使得生成的轨迹能够比这个上限更长。
隐私预算还原
本文引入稀疏向量的概念将隐私预算节省下来仅用于重大改变,给定在位置$s_i$的方向为$dir_i$,在给定在位置$s_{i+1}$的方向为$dir_{i+1}$,重大改变需满足$\Delta d i r=d i r_{i+1}-d i r_{i}<\theta$,本文设定偏差临界值$\theta=0.707$。更直观地来看,如果新一步的偏差角度大于$45^{\circ}$,即$\cos \left(\Delta \operatorname{dir}^{\circ}\right)<\theta$,认为运动目标的方向有了很大的改变,否则认为依然按照原方向运动。未有重大改变时撤回选定的位置$s_{i+1}$并保持在$s_i$的原方向来预测下一位置。
Evaluation
实验数据
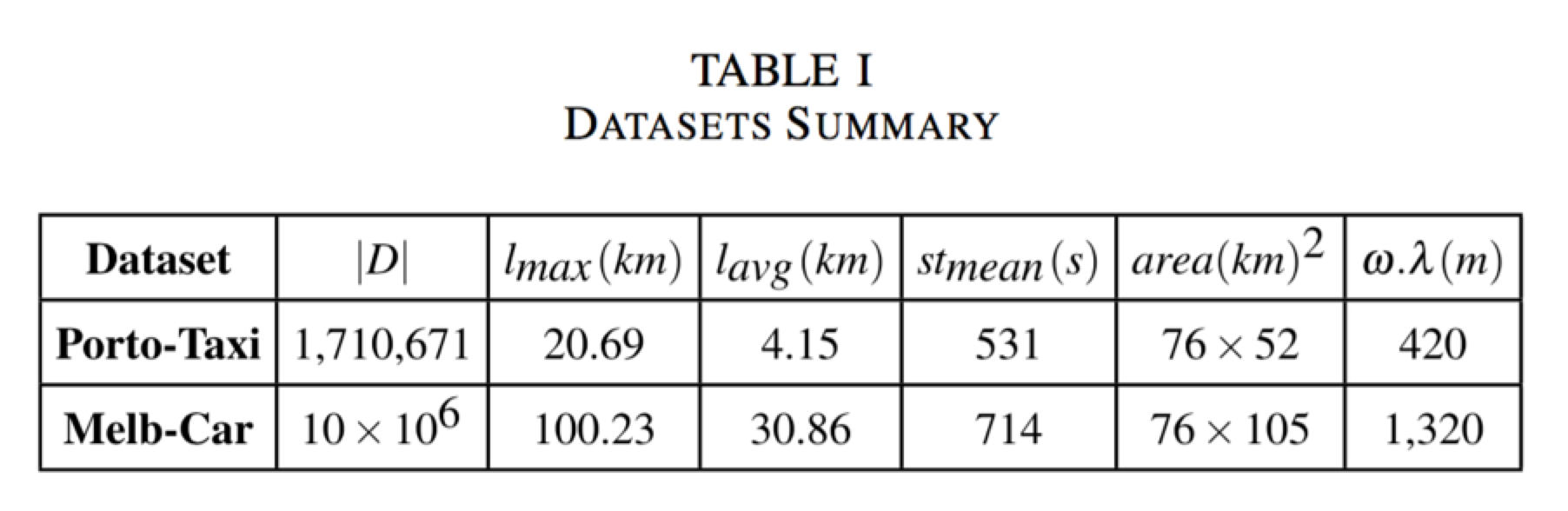
表一所列的是本文实验所用的两个数据集,Porto-Taxi提供了葡萄牙波尔图市的的士轨迹,Melb-Car是由Minnesota Web-based Traffic Generator生成的位于墨尔本的合成数据集。
TGM表现评估
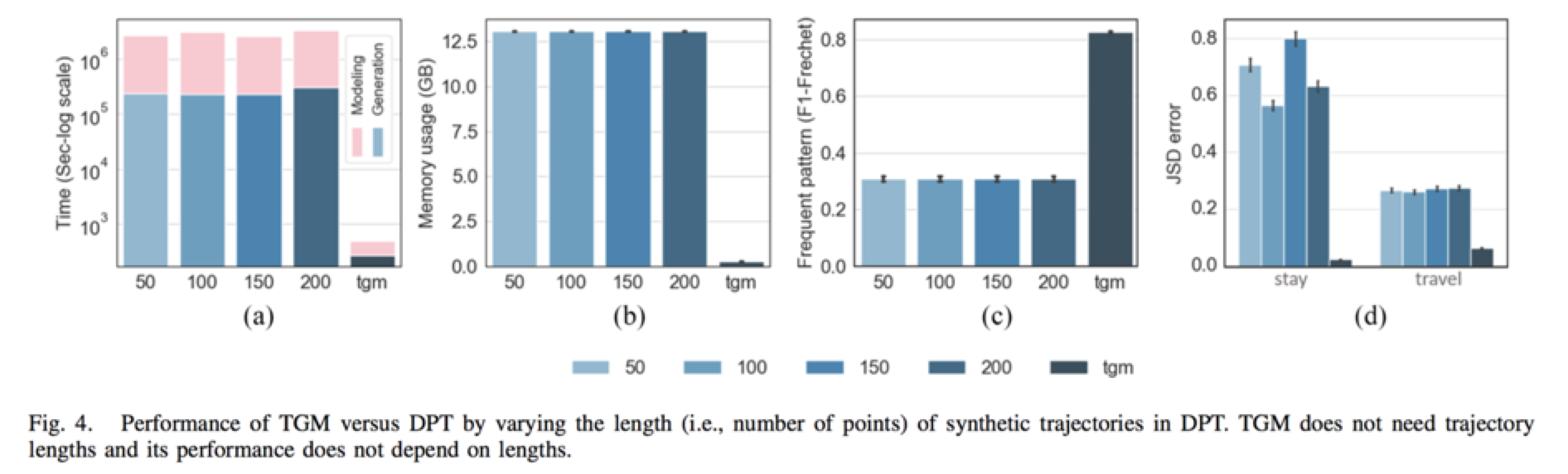
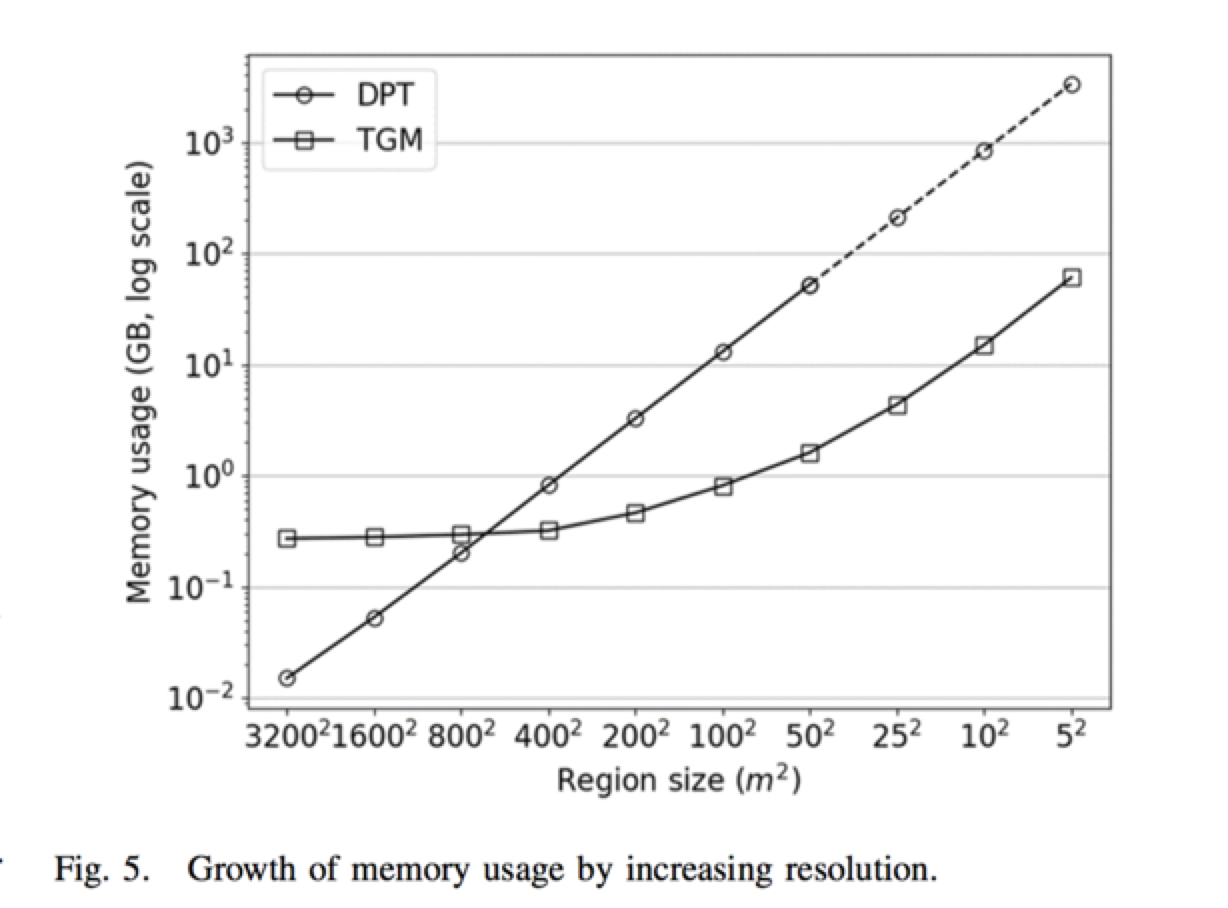
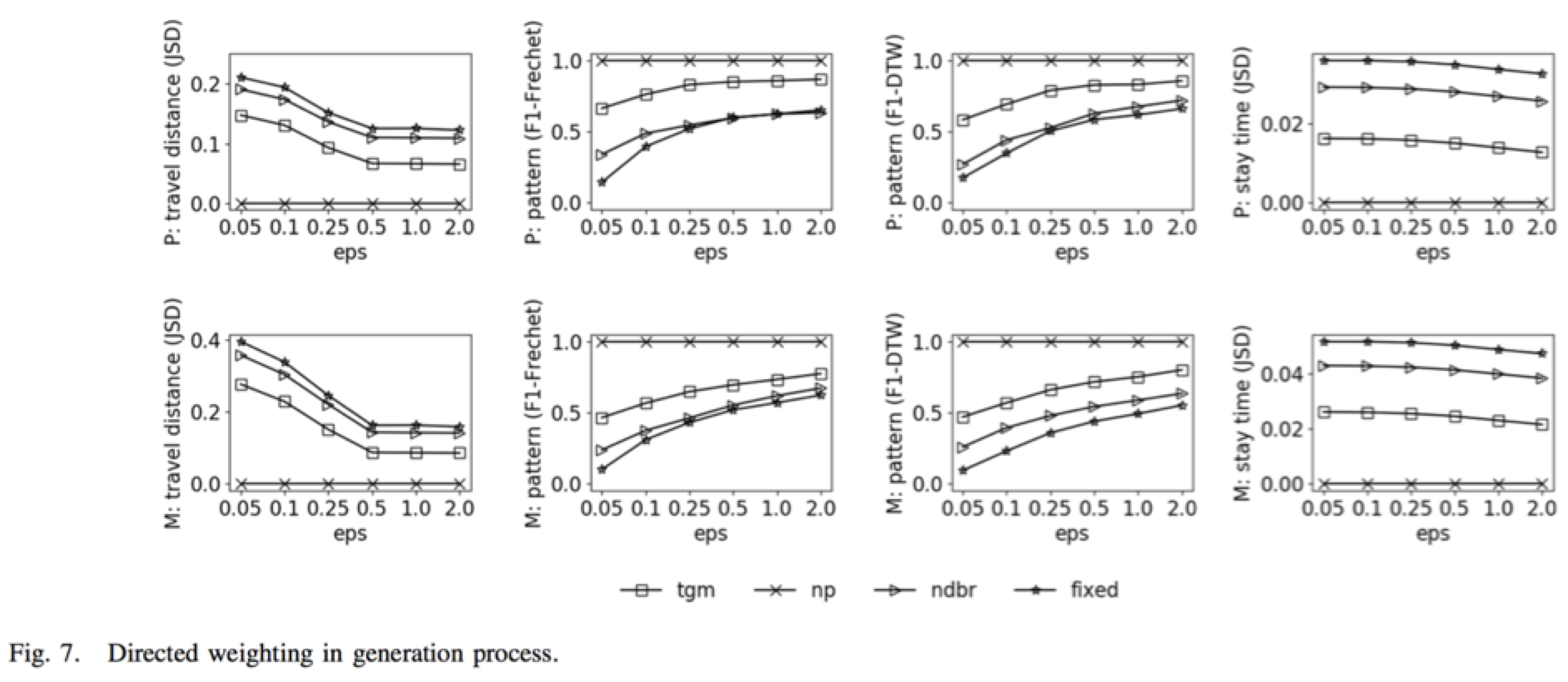
本文用TGM与DPT进行对比,DPT需要求用户指定合成轨迹的长度,而TGM能够动态地确认生成轨迹的长度。如图4所示,本文采样了Porto-Taxi中的十万条轨迹记录来对比TGM和DPT在运算速度、内存需求、Frechet距离和JS散度误差且TGM的表现均优于DPT。图5详细表明了随着网格尺寸变小(分辨率变大),TGM和DPT对内存需求的变化情况,TGM的内存需求随网格分辨率呈线性增长,而DPT则为指数增长。图7分析了使用适应性的预算分配方法和预算归还战略时TGM的效用的变化情况,np表示最优的结果以无隐私保护无噪声为基准线,ndbr是为包括隐私预算归还方法的TGM,fixed代表对每一步使用固定比例的来生成合成轨迹,结果中fixed和ndbr方法的较高的斜率表明这两种方法对所加的噪声更为敏感即缺乏鲁棒性,实验结果还表明了TGM对大都市的数据更为高效。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。


