这是知乎上的一道题目，题目链接为https://www.zhihu.com/question/397446056。本文尝试构造一个可能的解决方法。

题目描述

在酒店中（假设房间号是1到n之间的连续的自然数），每个人有一个自己的房间但是不知道别人的房间号码。如何在双方都不暴露自己房号的情况下判断和对方是否相邻？

注：问题的背景是我在酒店住宿，所有客人都在一个微信群里。我想在双方都不暴露自己房号的前提下确定谁是我的邻居。

问题可以思考以下两种情况：

线形酒店：若两个数字的差为1，则称为相邻。
环形酒店：若两个数字的差为1，或者这两个数字是1和n，则被称为相邻。

问题定义

我们先考虑线性酒店的邻居问题。假设有 $n$ 个用户，用户 $i$ 拥有的值为 $i$。参与方Alice和Bob分别用在 $x_A, x_B\in[n]$ 的房间中，我们需要判断 $|x_A - x_B|=1$ 是否成立。

对于这个问题，有以下的几点说明：

所有的用户需要按照协议的流程提供数据，并且对数据进行操作，但是用户可以尽可能猜测其他用户的数据。（显然，如果用户不遵守流程，一切都是没有意义的，比如用户C在1号房间，他偏说自己是在8号房间，就得不到正确的结果）

我们的协议中，传输信道是公开的。

任何人都可以计算任何两个用户是否相邻。

基于LDP的常见思路

在刘巍然的回答中（ https://www.zhihu.com/question/397446056/answer/1318293891）提到了两种基于LDP的解法，分别是：

Laplace 机制
基于离散采样的方法，本质是kRR

Laplace Mechanism

在这个数据中，我们可以知道数据的敏感度为：

$\Delta f=\max _{x,y \in [n]}||x-y||_{1}=n-1$

因此对于数据的加燥过程实际上就是这样了：

$x' = x + \operatorname{Lap}(\frac{n-1}{\epsilon})\\ y' = y + \operatorname{Lap}(\frac{n-1}{\epsilon})$

然后我们通过比较 $ x’,y’$来间接表示 $x,y$ 的差。这个问题在哪里呢，最大的问题在于随着 $n$ 的增大，Laplace的误差会出现明显的增大，本质是由于敏感度为 $n$。比如假设 $n=10, \epsilon=1$的话，噪声的分布就是这个样子了:

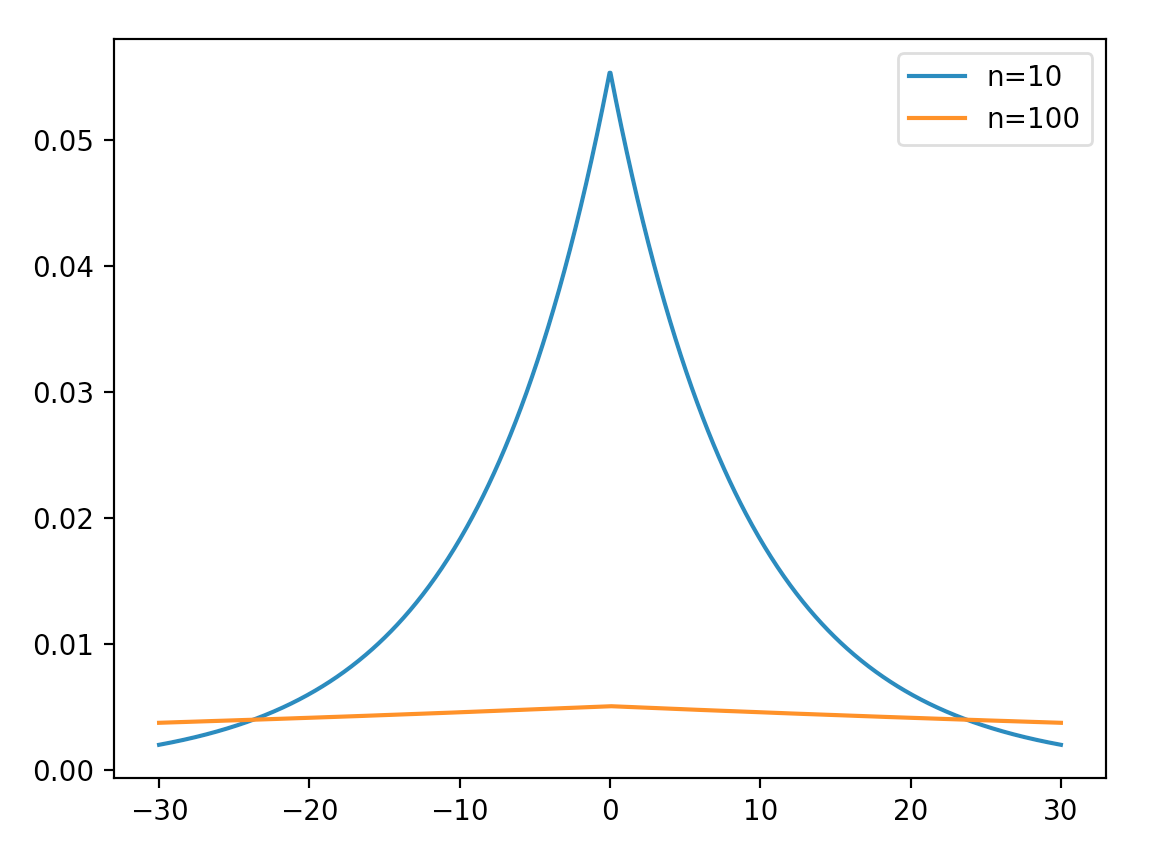
如果有 $n=100$ ，可以说几乎是均匀分布了。

基于k-Randomized Response

kRR是Randomized Response的扩展，其基本的编码机制为：

$\Pr[\mathcal{M}(x)=y] = \begin{cases} \frac{e^\epsilon}{e^\epsilon+k-1}, \quad &\text {if } y=x;\\ \frac{1}{e^\epsilon+k-1}\quad &\text {if } y\not=x. \end{cases}$

说人话，就是对于值$x\in[n]$，我们以概率 $\frac{e^\epsilon}{e^\epsilon+k-1}$ 说“我的房间编号是 $x$”，然后以其他的概率说房间编号是其他值。举个例子，假设一共有三个房间号，用户1的房间号是1，那么此时 $k=3$，用户1公开自己的房间编号概率分别为（w.p. 表示 with probability）：

$\begin{cases} 1, \quad\operatorname{w.p.}\quad 0.5761168847658291\\ 2, \quad\operatorname{w.p.}\quad 0.21194155761708547\\ 3, \quad\operatorname{w.p.}\quad 0.21194155761708547 \end{cases}$

那么我们可以明显地发现用户回答自己的概率其实是很小很小的，如果有100个用户的话，回答自己的值的概率仅仅为 $p=0.026723630989395224$。差不多也是不能用了。

基于BV的解决思路

这里我们给出一种基于Bit Vector+LDP 的方案，论文参考为：

BV的思路大概是这样子的，假设有个区间 $T$，那么对 $x$ 编码是，编码过程为：

$\operatorname{Encode}(x) = \begin{cases} 0,\quad\operatorname{if}\quad x \not\in T\\ 1,\quad\operatorname{if}\quad x \in T \end{cases}$

BV的核心在于：如果两个数很接近，那么他们就很可能同时出现在一个区间中，或者同时不出现在一个区间中。比如Alice的值是2，Bob的值是3，那么随便给一个区间长度为2的区间，大概率是Alice和Bob编码的结果同时在这个区间或者同时不在这个区间。这个同时在或者同时不在可以用汉明距离去衡量。

因此，BV有如下性质，假如数据分布范围为$[0,u]$，给定$s$ 个随机区间，那么两个数据差值可以这么估计：

$\left|x_1-x_2\right|=\frac{d_{H}(x_1', x_2') \cdot u}{2 s}$

其中，$d_H$ 表示汉明距离，$x_1’, x_2’$ 表示两个长为 $s$ 的比特向量。

因此，拟解决方案可以如下：

$n$ 个用户，每个用户生成 $k$ 个随机区间，这样一共生成了 $n\cdot k$ 个随机区间，可以假定每个区间的长度为2。

每个用户真实回答一个 $n\cdot k$ 的比特向量，表示当前用户的值是否在对应的区间。

按照BV的方法，任何用户可以估计任何其他两个用户A和用户B的差。

当然，这里是有问题的，问题的根本在于什么呢，在于接收到数据的人是同时知道 $T,\operatorname{Encode}(x)$ 的，举个例子，我都知道区间是 $[1,5, 3.5]$，和编码结果是1了，我当然知道你的值 $1.5\le x \le 3.5$了。

所以我们要减弱通过 $T,\operatorname{Encode}(x)$ 推出 $x$ 的能力，我们通过随即响应的方式，加上这么一层随机响应：

$n$ 个用户，每个用户生成 $k$ 个随机区间，这样一共生成了 $n\cdot k$ 个随机区间，可以假定每个区间的长度为2。

每个用户暂时得到一个 $n\cdot k$ 的比特向量，表示当前用户的值是否在对应的区间。

对于每一位，用户以概率 $p$ 对在不在某个区间进行随机响应。

任何用户可以估计任何其他两个用户A和用户B的差。

我们可以证明，这个新的机制是满足 $(\epsilon, \delta)$-LDP的，并且有：

$\delta=\left(\frac{e^{\epsilon}}{e^{\epsilon}+1}\right)^{s}-e^{\epsilon} \cdot\left(\frac{1}{e^{\epsilon}+1}\right)^{s}$

这时候，两个数据的差可以这么估计：

$|x_1-x_2|=\frac{\mu}{2 s} \cdot\left(\frac{e^{\epsilon}+1}{e^{\epsilon}-1}\right)^{2} \cdot d_{H}-\frac{\mu\cdot e^{\epsilon}}{\left(e^{\epsilon}-1\right)^{2}}$

当然，任何基于LDP的方案本质上都是在可用性和隐私性之间的权衡，永远做不到数据100%的精确。