最近从零开始学习了树模型，因此做一个记录。最终目标是学习GBDT，但是之前没有了解过树模型，学习的过程遇到了一些困惑，比如：

只对决策树有个基本印象，会不会很难学？
决策树是用来分类的，怎么树还能搞回归呢？
Bagging、Boosting各种专有名词听起来就很高级，感觉自己很慌！
CART、GBDT、XGBoost、各种模型傻傻分不清楚。。。

所以本篇内容的目的是一篇文章把基本脉络搞清楚，大概的路线是：

决策树：从分类树到CART回归树
集成学习：Boosting V.S. Bagging

决策树

CART 回归树

CART 全称叫做 classification and regression tree，分类与回归树。可以同时用于分类和回归任务。假如现在已经有一棵CART树了，那么预测的过程可以这么理解：

$f(x) = \sum_{m=1}^M c_mI(x\in R_m)$

其中 $I(x\in R_m)$ 表示指示函数，如果 $x\in R_m$则函数值为1，否则为0。也就是说我们假设每个叶子节点有一个权重，如果数据属于这个叶子节点，那么预测结果就是对应叶子节点的权重。通过这种方法，树就可以用于回归。

假如给定数据 $(x_1,y_1),…,(x_n,y_n)$，CART采用平方误差来衡量loss，即希望：

$\min \sum_{i=1}^n\left(f(x_i)-y_i\right)^2$

类似于决策树，我们通过所谓的“分裂”的方式构建树。假如现在给一个根节点，所有的数据都在根节点，那么我们怎么把数据分成两堆？简单的思路就是：我们对当前可能的分裂属性和对应属性的分裂值进行遍历，选择拆分后平方和最小的结果作为分裂结果。比如当前的数据有性别和年龄，那么我们不知道选哪个属性，也不知道选了对应属性之后怎么分二叉树，所以我们先试着先按性别划分，再试着按年龄划分，年龄划分中，我们对所有可能的年龄进行划分，然后找到最小的loss对应的划分。因此，划分过程就是：

$\min _{s}\left[\min _{c_{1}} \sum_{x_{j} \in R_{1}}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}}\left(y_{i}-c_{2}\right)^{2}\right]$

很简单可以证明，对于数据 $y_1,…,y_n$，使得 $\sum_{i=1}^n (y_i-c)^2$最小的 $c$ 取值为：$c = \frac{1}{n}\sum_{i=1}^n$（求导等于0就可以算出来），因此知道树的划分之后，叶子节点的权重就是当前叶子节点上数据的均值。因此理解上，CART回归树算法就有了，如下图所示：

CART回归树

上图来源于《统计学习方法》。

集成学习：Bagging V.S. Boosting

集成学习，也就是 Ensemble Learning，英文名字很高级，实际上思路没有那么复杂。个人理解就是：俗话说，三个臭皮匠，顶个诸葛亮。那么我们是不是几个简单的模型合在一起就可以发挥出很厉害的功能，可以媲美复杂模型呢？所以出来了两种模型融合的思想：可以将弱分类器融合之后形成一个强分类器，而且融合之后的效果会比最好的弱分类器更好。

在此基础上，诞生了两类方法，分别是Bagging和Boosting。

Bagging

Bagging的思路很简单，模型复杂度不够，那就数量来凑，就是最基本的三个臭皮匠，顶个诸葛亮。他的思路可以分为这么三步：

从原始样本当中，有放回地抽取 $n$ 个样本，形成一个训练集。并且按照这个过程形成 $K$ 个独立的训练集。
分别用 $K$ 个训练集形成 $K$ 个不同的模型。
对于分类问题，用 $K$ 个模型投票最多的作为结果，对于回归问题，用 $K$ 个模型的均值作为结果。

Boosting

Boosting的思路和Bagging有点不同，不是采用互相独立的模型来进行效果提升。更像是我们学习当中的“错题本”思路：首先做题，然后把错误的题目拿出来再回顾一下，以此类推。所以Boosting的大致过程为：

对所有数据进行学习，获得一个基学习器；
根据基学习器的学习效果，获得残差（预测值与真实值的差）；
对残差进行学习；
重复上述过程，依次对残差进行学习，建立$K$个模型。

Bagging V.S. Boosting

Bagging方法最大的特点是不同的学习器之间相互独立，可以并行地预测。代表方法是：随机森林（Random Forest）。

Boosting个体学习器之间存在很强的依赖关系，只能串行进行学习。代表方法是：AdaBoost、GBDT、XGBoost。

Bagging 与 Boosting 都是一种集成学习，可以将弱的学习器提升为强的学习器。

从CART到GBDT

提升树

我们把以决策数为基函数的 Boosting 方法叫做提升决策树，Boosting Tree。提升树可以表示为多个决策数相加，假如有 $M$ 棵树，第 $m$ 棵树为 $T_m$，那么提升树可以用加法模型表示为：

$f_{M}(x) = \sum_{i=1}^M T_m(x)$

也就是说，后一棵树学习到的是前面的树的残差。提升树的算法如下：

初始化$f_0(x) = 0$
对于 $m = 1, 2, …, M$，依次学习树 $T_m$：
- 计算残差 $r_{m,i} = y_i - f_{m-1}(x_i)$
- 学习树 $T_m$ 对 $r_{m,i}$ 拟合
- 更新 $f_m(x) = f_{m-1}(x)+T_m(x)$
得到提升树：$f_{M}(x) = \sum_{i=1}^M T_m(x)$

GBDT

前面我们介绍了CART用于回归，它采用了平方误差，也很容易理解，但是存在这么一个问题：对于一个更一般的损失函数，怎么设计CART树？这个就显得不那么容易了。然后就有了GBDT的思想。

GBDT全称是Gradient Boosting Decision Tree，叫梯度提升决策树，首次由Jerome H. Friedman在论文《 Greedy function approximation : A gradient boosting machine》中提出。从名字可以看出GBDT有两个特点：

梯度 Gradient
提升 Boosting

所以接下来主要看：梯度Gradient和提升Boosting如何用于构建树的！Boosting的思路就很简单了，重点是Gradient，这玩意和残差是啥关系呢？实际上GBDT用负梯度来近似模拟残差。

所以GBDT的最终过程就是这样的：

初始化学习器：
$f_0(x) = \arg\min_c \sum_{i=1}^nL(y_i,c)$
开始迭代训练 $m=1,…,K$ 棵树：
- 对每个样本计算负梯度用于下降
  $r_{m,i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f x)=f_{m-1}(x)}$
- 将 $(x,r_{m,i})$ 作为当前树的训练数据，得到回归树，其中，回归树有 $J$ 个叶子节点，对应 $J$ 个区域
- 对回归树的叶子节点计算权重：
  $c_{m j}=\arg \min _{c} \sum_{x_{i} \in R_{m j}} L\left(y_{i}, f_{m-1}\left(x_{i}\right)+c\right)$
- 更新学习器：
  $f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J} c_{m j} I\left(x \in R_{m j}\right)$
得到最终的学习结果GBDT模型：
$\begin{align} f(x) &= f_0(x) + ... + f_M(x)\nonumber\\ &= f_0(x) + \sum_{m=1}^M\sum_{j=1}^J c_{m,j}I(x\in R_{m,j})\nonumber \end{align}$

我们以平方误差举个例子：$L(y,f(x))=\left(x-f(x)\right)^2$，那么对于初始化的过程，有：

$f_0(x) = \arg\min_c \sum_{i=1}^nL(y_i,c) =\frac{1}{n} \sum_{i=1}^n y_i$

然后有：

$\begin{align} r_{m,i}=-\left[\frac{\partial L\left(y_{i}, f\left(x_{i}\right)\right)}{\partial f\left(x_{i}\right)}\right]_{f x)=f_{m-1}(x)} = 2\left(y_i - f_{m-1}(x_i)\right)\nonumber \end{align}$

以及在叶子节点权重的计算过程中，有：

$\begin{align} c_{m_j} = \frac{1}{a} \sum_{i=1}^a \left(y_i - f_{m-1}(x_i)\right) = \frac{1}{a} \sum_{i=1}^a r_{m_j}\nonumber \end{align}$

至于 GBDT 如何用于二分类、多分类以及如何实现GBDT，如果日后还需要就再详细介绍。

核心问题来了，残差好好的，为啥要搞个梯度去学习呢？目前（2021年11月30日），我还没有找到能很好地说服我的回答。而且计算叶子节点的权重如果不是平方误差的话也不好算啊。

XGBoost

最优化目标

前面的CART模型也好，GBDT模型也好，在进行优化的过程中，只考虑了 loss 函数这一项，没有考虑到模型复杂度带来的影响（比如过拟合之类）。如果综合考虑样本的 loss 和树本身带来的复杂度（用 $\Omega(f_k)$ 表示第$k$ 棵树的复杂度），那么优化目标可以写作；

$Obj = \sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}\right)+\sum_{k} \Omega\left(f_{k}\right)$

假设有 $K$ 个树，那么学习过程可以这么认为

$\begin{align} \hat{y}_{i}^{(0)} &=0 \nonumber\\ \hat{y}_{i}^{(1)} &=f_{1}\left(x_{i}\right)=\hat{y}_{i}^{(0)}+f_{1}\left(x_{i}\right) \nonumber\\ \hat{y}_{i}^{(2)} &=f_{1}\left(x_{i}\right)+f_{2}\left(x_{i}\right)=\hat{y}_{i}^{(1)}+f_{2}\left(x_{i}\right) \nonumber\\ & \cdots \nonumber\\ \hat{y}_{i}^{(t)} &=\sum_{k=1}^{t} f_{k}\left(x_{i}\right)=\hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\nonumber \end{align}$

也就是第 $t$ 个树预测的东西是 $\hat{y}_{i}^{(t)}=\hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)$。

目标之中的 loss

如果我们暂时先不考虑约束项，那么目标可以写成：

$\begin{align} O b j^{(t)} &=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t)}\right)=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)\nonumber \end{align}$

如果我们的loss选取的是二次loss，那么就有：

$\begin{align} O b j^{(t)} &=\sum_{i=1}^{n}\left(y_{i}-\left(\hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)\right)^{2} \nonumber \\ &=\sum_{i=1}^{n}\left[2\left(\hat{y}_{i}^{(t-1)}-y_{i}\right) f_{t}\left(x_{i}\right)+f_{t}\left(x_{i}\right)^{2}\right]\nonumber \end{align}$

这个当中 $(\hat{y}_{i}^{(t-1)}-y_{i})$ 表示的就是残差。然后我们回想一下泰勒展开式：

$f(x+\Delta x) \simeq f(x)+f^{\prime}(x) \Delta x+\frac{1}{2} f^{\prime \prime}(x) \Delta x^{2}$

把泰勒展开中这么进行一下类比，把 $f(x)$ 看成 $l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)$，然后 $\Delta x$对应 $f_t(x_i)$。所以我们就可以令：$g_{i}=\partial_{\hat{y}^{(t-1)}} l\left(y_{i}, \hat{y}^{(t-1)}\right), \quad h_{i}=\partial_{\hat{y}^{(t-1)}}^{2} l\left(y_{i}, \hat{y}^{(t-1)}\right)$，那么就有：

$O b j^{(t)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]$

这个对函数求导，不太容易看得懂，举个例子，对于平方误差，有：

$\begin{align} g_{i}&=\partial_{\hat{y}^{(t-1)}}\left(\hat{y}^{(t-1)}-y_{i}\right)^{2}=2\left(\hat{y}^{(t-1)}-y_{i}\right) \nonumber\\ h_{i}&=\partial_{\hat{y}^{(t-1)}}^{2}\left(y_{i}-\hat{y}^{(t-1)}\right)^{2}=2\nonumber \end{align}$

因为在构建当前树的过程中，前面的树是构建好了的，也就是$l(y_{i}, \hat{y}_{i}^{(t-1)}) $ 是固定大小的，所以现在的目标就是最小化这个东西：

$\sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]$

假如我们已经产生一棵树了，那么这个 $f_t(x_i)$ 就是对应叶子节点的权重了，可以认为：

$f_t(x) = w_{q(x)}$

其中，$q(x)$ 表示 $x$ 对应的是第几个叶子节点，总的叶子节点数记为 $T$，因此 $q:\mathcal{X}\rightarrow \{1,2,…,T\}$，$\mathcal{X}$ 表示输入空间。

树模型的复杂度

刚才是一直没考虑到模型的复杂度的，现在我们重新看模型的复杂度，比如我们可以这么定义模型复杂度：

$\Omega\left(f_{t}\right)=\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2}$

其中，$T$ 表示叶子节点的个数，然后 $\gamma,\lambda$ 是超参数，$w_j$表示第 $j$ 个叶子的权重。比如下面这个树的复杂度就在下图中描述。

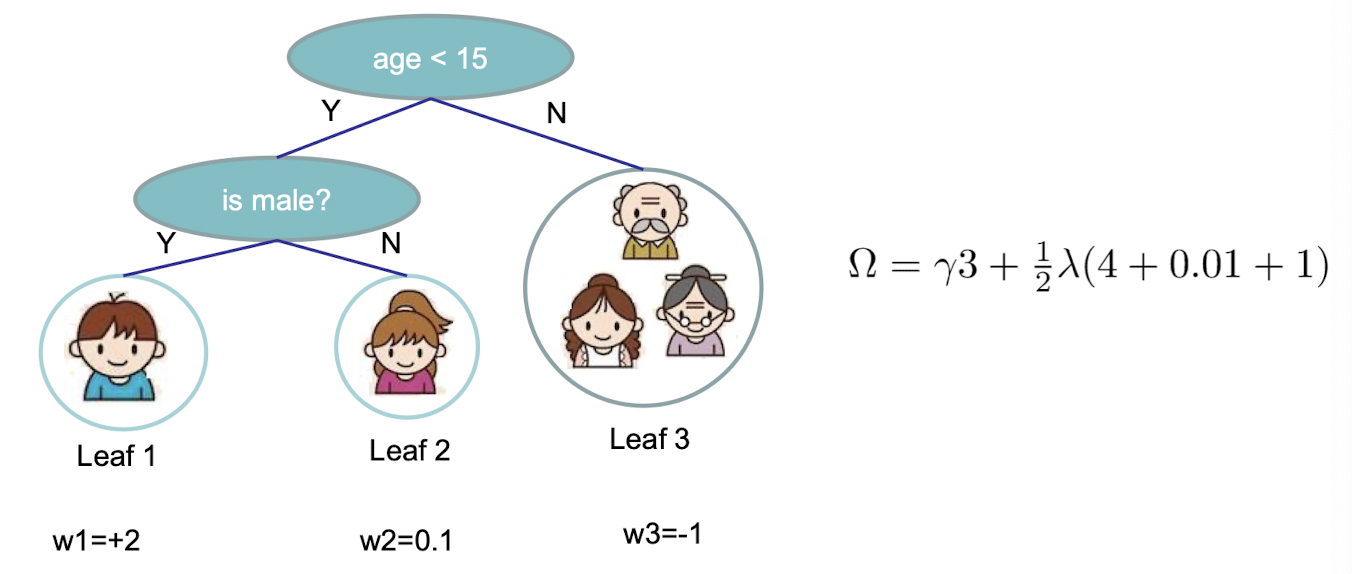
因此现在的核心目标可以表示为：

$\begin{align} Obj &= \sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)\nonumber\\ &= \sum_{i=1}^{n}\left[g_{i} w_{q\left(x_{i}\right)}+\frac{1}{2} h_{i} w_{q\left(x_{i}\right)}^{2}\right]+\gamma T+\lambda \frac{1}{2} \sum_{j=1}^{T} w_{j}^{2}\nonumber \end{align}$

上面的公式相当于对 $n$ 个数据依次求loss，注意到这 $n$ 个数据是最终分布在 $T$ 个叶子节点上的，所以我们可以把在同一个叶子上的数据放在一起，进行一个 Group，所以有：

$I_j = \{i | q(x_i)=j\}$

也就是 $I_j$ 表示第 $j$ 个叶子节点上的数据集合。比如 $I_1 = \{1,2,5\}$ 表示 $x_1,x_2,x_5$ 在第一个叶子节点上。然后可以把 Obj 进行一个转换：

$Obj =\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T$

这时候回想一下初高中的一元二次方程，就是看上面那个中括号中的东西，在假设有这个树的情况下，令 $G_j=\sum_{i \in I_j} g_i, H_j=\sum_{i \in I_j}h_i+\lambda$，那么上面这个东西的中括号里面就是 $Gw + \frac{1}{2}Hw^2$，要想这个东西达到最小，那么有

$w = -\frac{G}{H}, \quad \min\left(Gw+\frac{1}{2}Hw^2\right)=-\frac{1}{2}\frac{G^2}{H}$

所以现在的目标就是：

$\begin{aligned} O b j^{(t)} &=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T \nonumber\\ &=\sum_{j=1}^{T}\left[G_{j} w_{j}+\frac{1}{2}\left(H_{j}+\lambda\right) w_{j}^{2}\right]+\gamma T\nonumber \end{aligned}$

其中的最优解是

$w_j^* = -\frac{G_j}{H_j+\lambda}, \quad Obj=-\frac{1}{2}\sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{i}+\lambda}+\gamma T$

所以现在就相当于：我们只要知道树的当前结构，我们就知道叶子节点中的权重是多少，也知道当前的Obj是多少了。比如下面这个图：

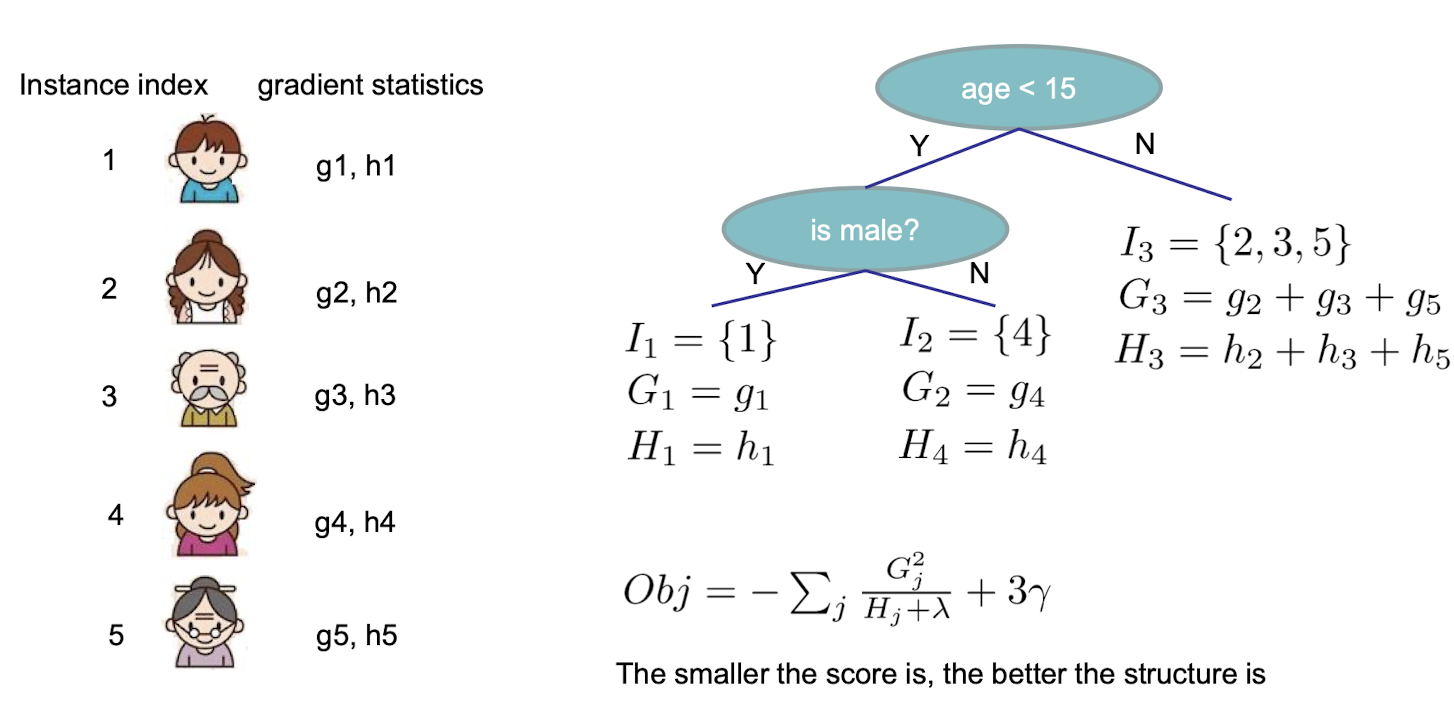
所以根据上面的思路，我们好像就可以构建树模型了，以下是一个方法：

枚举所有可能的树模型
多每个模型，求出当前模型的 Obj
找到 Obj 最小的那个模型，然后更新叶子的权重为 $w_j^*$

想法很美好，现实很残酷，因为第一步的枚举所有树模型是不太可能实现的。但是没办法，树还是得去构建，于是我们想到了决策树的四箱，用贪心的方法去一次次找到分裂特征的方法来构建树。我们尝试去看，如果对于把一个叶子节点分开了，那么我们获得了多少所谓的收益呢？联合上面的Obj，用$Obj(0),Obj(1)$表示分列前和分裂后的Obj，那么有：

$\begin{align} Obj(0) &= -\frac{1}{2}\frac{G}{H+\lambda} + \gamma\nonumber\\ Obj(1) &= -\frac{1}{2}\left(\frac{G_L}{H_L+\lambda} + \frac{G_R}{H_R+\lambda}\right) + 2\gamma\nonumber \end{align}$

这个当中，有 $G=G_L+G_R$。因为在构建的过程中，这个Obj是要越来越小的，所以这里的收益Gain就是：

$\begin{align} Gain &= Obj(0) - Obj(1)\\ &= \frac{1}{2}\left(\frac{G_L}{H_L+\lambda} + \frac{G_R}{H_R+\lambda} - \frac{G_L+G_R}{H_L + H_R+\lambda}\right)- \gamma \end{align}$

也就是说，我们要是希望Obj可以更快地下降，那么希望每次分裂的时候Gain尽可能地大就好了。看上去好想知道怎么分了，但是其实也没完全说明白。假如当前叶子中有 $100$ 个数据，那么我们怎么把这个数据分两堆？这复杂度可不低的。

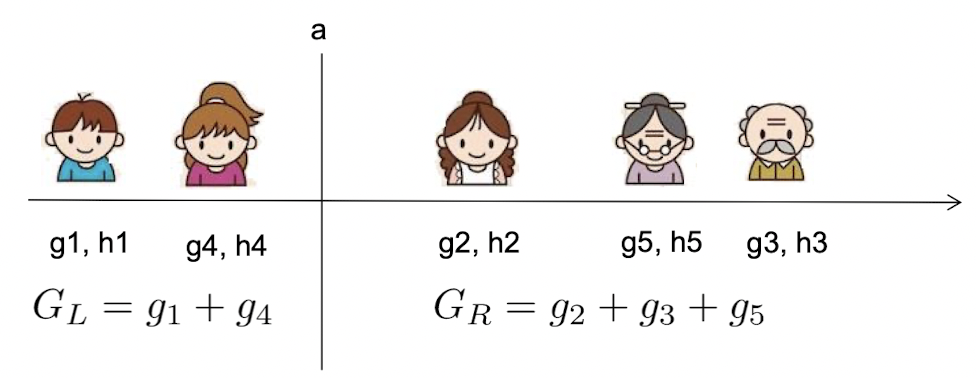
所以我们不能随便分，我们用一种线性搜索的策略：我们把当前叶子节点中的数据进行排序，然后从排好序的数据中找到一个分裂点使得当前Gain最高。这样复杂度就不高了。

所以目前的构建树的策略是：

（1）构建根节点，所有的数据都在根节点上
（2）对于每个节点，按照以下方法枚举每个特征：
- （2.1）对于每个特征，对节点的数据进行排序
- （2.2）采用线性搜索策略找到当前特征下最好的分裂节点
- （2.3）找到当前节点最好的分裂策略
（3）选择最好的节点进行分裂

按照上面的这个方法，我们就可以把树构建出来了。

复杂度分析，现在简单分析一下模型的复杂度，每一层我们都需要 $O(n\log n)$进行排序，然后有 $d$个特征，同时我们想要构建的深度是 $K$，所以构建树模型的复杂度是 $O(n\cdot d \cdot K\log n)$。作者的PPT里面说还可以进行优化。然后这个方法对于数据量很大的情况也能很快地进行收敛。

加速构建模型：Bucket

为了说明问题，构建树的策略重复描述一遍：

（1）构建根节点，所有的数据都在根节点上
（2）对于每个节点，按照以下方法枚举每个特征：
- （2.1）对于每个特征，对节点的数据进行排序
- （2.2）采用线性搜索策略找到当前特征下最好的分裂节点
- （2.3）找到当前节点最好的分裂策略
（3）选择最好的节点进行分裂

主要的流程是（2.1）—（2.3）步骤，其核心思想就是要找到一个特征值，并且按照这个特征值把当前的数据分成左右两部分，再看这个分的好不好。因为当前不知道按照什么值分，所有就对所有的数据遍历一遍，看看哪个效果好。假如我们当前的数据表示的是用户的年龄，分布在1-100之间，那么当前的方法就会从1到99依次试一下，然后找到最好的分裂策略。这个方法是没问题的，但是穷举的过程中会消耗较高的计算资源，并且从理解上，人为感觉，以50为分界线和以51为分界线好像也没有很大的区别。

所以在实现的过程中，有一个叫做分桶的策略：Bucket。在某一个特征的遍历过程中，我们先对这个特征进行分桶，依然以年龄为例，我们可以把年龄分成以下几个部分：

$\operatorname{Age} = \{0-25, \quad 25-50, \quad 50-75, \quad 75-100\}$

有了这个“背景知识”，所有的数据只需要安心地知道自己在哪个桶就好了，所以也就不需要每次的排序过程了。然后在分裂的时候，只需要尝试三次不同的分裂值，分别是：Age=25, Age=50, Age-75。所以，分桶数量越少，计算越快，但是越不准确，分桶数量越多，数据精度越高，带来的计算也更复杂。值得注意的是，分桶这个操作是可以并行的，桶内的 g 和 h 的求和可以提前算出来。