论文阅读-Towards Practical Differential Privacy for SQL Queries

文章地址：https://ieeexplore.ieee.org/document/9488825/
标题：AdaPDP: Adaptive Personalized Differential Privacy
作者：Ben Niu, Yahong Chen, Boyang Wang, Zhibo Wang, Fenghua Li, Jin Cao

这篇文章提出了自适应的个性化DP机制，用于提升数据效用。其核心证明过程认为依据设计的采样概率对数据进行采样，如果数据没有被采样则该数据没有泄露隐私。笔者仔细思考了一下，认为此论文的核心假设和证明过程是错误的。本篇文章后面也附有我对此论文的疑问。我曾把文章疑问转发给了中科院的牛犇老师，老师第一时间转发给了作者Yahong Chen同学，但未得到回复，可能是教育邮箱作者平时不太关注。如果有读者认为此过程是正确的，欢迎与我进行讨论。我的联系方式可在公众号进行获取。

先简单梳理一下本文总的脉络吧，论文结构分为9个章节，如下：

• dd

摘要

当用户的个人数据被收集形成数据集的过程中，用户通常会有不同的隐私保护需求。为了跟踪此问题，不同个性化差分隐私（Personalized differential privacy, PDP）被提出用于统计信息发布。然而，当前的一些方法的数据效用较低，主要是由于以下两点：1）某些用户被过度保护；2）数据效用在目标设计阶段没有考虑。低数据效用阻碍了人们对RDP的采用。本文呈现了自适应性个性化差分隐私框架，称为AdaPDP。为了最大化不同场景下的数据效用，AdaPDP适应地选取噪声产生算法，并且根据请求类型、数据分布和隐私设置计算对应参数。此外，AdaPDP采用了多轮的utility-aware采样以满足不同用户的隐私需求。本文的隐私分析表明提出的框架具备严格隐私保护。我们也执行了大量的实验表明所提出方法的有效性。

Introduction

由于智能手机、5G和物联网设备的快速适配，很多服务提供商从个人用户那里收集数据，并允许第三方（本文称为请求者）通过提交各种查询来了解所有用户数据的统计信息 . 例如，医院可以收集患者的医疗数据，并允许第三方研究人员从其数据集中学习所有患者的统计信息，以便进行药物研究。 但是，用户经常担心他们的隐私，不希望请求者了解他们的敏感数据。 此外，不同的用户可能有不同的隐私需求，其中一些用户的限制非常严格，而另一些用户则相对宽松。

个性化差分隐私（PDP）被提出来解决用户的不同隐私需求。 PDP 允许服务提供商从用户那里收集数据，并根据每个用户的个人隐私预算定制对来自请求者的查询进行响应。尽管 PDP 取得了实质性进展，但依然有一些局限性。即，当前的 PDP 机制对请求者产生的查询结果准确性低。这主要是因为 (1) 一些 PDP 机制对用户隐私进行了过度保护导致数据效用降低； (2) 数据效用未明确包含在设计目标（Objective）中。低准确性导致数据效用差，并阻碍其他人利用数据集的信息。解决这个限制并非易事。在PDP中，每个用户自己设置自己的隐私预算。为了满足不统一的隐私要求，一些用户的预算可能会被浪费，从而导致效用损失。简单地减少预算浪费以提高数据效用可能很容易损害用户的隐私，尤其是对于隐私预算较低的用户。换句话说，设计 PDP 机制的挑战是如何在不损害所有用户的非统一隐私要求的情况下减少预算浪费。

本文为了应对这些挑战提出了一种自适应的个性化差分隐私框架，称为 AdaPDP。与以往的研究相比，我们提出的框架首先自适应地选择底层噪声生成算法，并根据查询函数的类型、数据分布和隐私设置计算相应的参数。我们的直觉是不同的情况（包括查询功能、数据分布和隐私设置）对数据效用有不同的影响。例如，基于拉普拉斯的噪声生成算法在某些情况下（查询函数具有较大的全局敏感度时）可能会产生高噪声。其次，与现有的单轮采样机制导致高预算浪费不同，我们提出的效用感知采样机制（utility-aware sampling）通过利用多轮采样，重复使用浪费的预算的方式来提高数据效用而不影响隐私保护。此外，它计算每轮的最佳采样阈值，以进一步提高数据效用。系统模型和本文框架图 1 和图 2 所示。本文的主要贡献如下：

• 本文提出了新的PDP框架称为AdaPDP。其根据请求函数，数据分布和隐私设置来提升数据效用；
• 本文设计了utility-aware采样机制来重新利用浪费的隐私预算，此方案可以提高数据效用；
• 我们严格证明了utility-aware采样机制的隐私保护特性；
• 本文在生成数据集和真实数据集上进行了大量的实验证明所提出方案相对于已有方案的有效性。我们也表明本文所提出的框架可以用在不同的查询函数上，如 average，count，median和逻辑回归。尽管前三个查询函数很简单，他们在构建复杂算法上是非常基本的。

Background

System Model

系统模型如图1所示，包括用户、服务提供商和请求者。每个用户把自己的数据 $d_i$ 和个人隐私预算 $\epsilon_i$ 发送给服务提供商。因此服务提供商有敏感数据 $D=\left\{d_{1}, \cdots, d_{n}\right\}$ 和用户的隐私等级 $\mathcal{S}=\left\{\epsilon_{1}, \cdots, \epsilon_{n}\right\}$ 两个集合。然后数据请求者想提供商发送请求来获取到数据的统计信息。这些请求比如有 average，count，median或者逻辑回归等等。

在此模型中，我们假设请求者既不被用户信赖，也不被服务提供商信赖。也就是说，请求者可能通过查询结果对数据进行一些推断，因此服务提供商需要对用户的数据进行保护。对于不同用户来说，其希望服务提供商可以提供 $\epsilon_i$的保护程度。

Differential Privacy

此小节介绍了DP的概念，提到了Laplace机制和指数机制，同时还提到了一个叫做 Subsample-and-Aggregate算法。

Subsample-and-aggregate算法 此算法将数据集 $D$ 分成等大小的 $k$ 个block，然后对每个block进行查询$f$ 得到查询结果，没个结果都是对整个数据集的估计，这样就获得了 $k$ 个估计结果。然后这 $k$ 个估计再采用一个满足DP的 aggregation 函数 $G$ 进行整合，作为 $f(D)$ 的最终结果。

Personalized Differential Privacy

PDP下每个用户 $u_i$ 有自己的隐私预算 $\epsilon_i$，所有用户数据的隐私预算集合用 $\mathcal{S}=\left\{\epsilon_{1}, \ldots, \epsilon_{n}\right\}$ 表示。PDP的严格定义为：

定义2：Personalized Differential Pirvacy: 给定 $\mathcal{S}=\left\{\epsilon_{1}, \ldots, \epsilon_{n}\right\}$ 和 $\mathcal{U}=\left\{u_{1}, \ldots, u_{n}\right\}$，随机化机制 $\mathcal{M}: \mathcal{D} \rightarrow R$ 是满足 $S$-PDP 的如果任意相差 $u_i$ 的相邻数据集 $D, D^{\prime} \in \mathcal{D}$ 和输出 $O \in R$，有$\Pr[\mathcal{M}(D) \in O] \leq e^{\epsilon_{i}} \times \Pr\left[\mathcal{M}\left(D^{\prime}\right) \in O\right]$

采样机制 Sampling 可以从完整的数据集中选择出一个子集。对采样的数据集进行查询而非对整个数据集进行查询可以提高请求结果的随机性并且保护数据隐私。许多PDP机制当中利用了采样作为关键技术。采样机制（Sampling Mechanism）可定义为

定义3：Sampling Mechanism 给定查询 $f: \mathcal{D} \rightarrow R$，数据集$D \subset \mathcal{D}$，采样阈值 $t$ 和隐私保护参数 $\mathcal{S}=\left\{\epsilon_{1}, \ldots, \epsilon_{n}\right\}$。令 $R S(D, \mathcal{S}, t)$ 表示按照以下概率对 $D$ 中每条数据进行采样：

$$\pi_{i}(t)=\left\{\begin{align} \frac{e^{\epsilon_{i}}-1}{e^{t}-1} & \quad \text { if } \epsilon_{i}<t \\ 1 & \quad\text { otherwise } \end{align}\right.$$

则采样机制可表示为：$S M_{f}(D, \mathcal{S}, t) \leftarrow D P_{t}^{f}(R S(D, \mathcal{S}, t))$，其中 $D P_{t}^{f}$ 是对于 $f$ 的任意一种满足 $t$-DP 的机制。

Adaptive Personalized Differential Privacy

AdaPDP总览 AdaPDP的总览如图2所示，其输入为敏感数据集 $D$，用户隐私预算 $S$ 和请求函数 $f$。PDP 首先根据请求函数选取噪声生成算法。然后噪声生成算法在本文提出的utility-aware采样机制中进行DP计算，同时我们也计算了最佳参数的具体大小。最后，根据选择的噪声生成机制和参数，此框架进行多轮计算使得数据效用最大化。

Limitation in Current Sampling Mechanism

我们首先分析了定义3的采样机制的不足。采样机制引入了两个方面的随机性：1）采样随机性，即某个数据不一定会被采样到；2）噪声随机性：即为了满足DP要求，需要添加噪声。这两种随机性将会导致两种误差：

• 采样误差：采样误差表示的是采样数据上的请求结果和全量数据上的请求结果的误差。总的来说，采样的数据越多，那么采样误差就越小。
• 噪声误差：在噪声误差方面，隐私限制越高则噪声带来的误差越大。

然后我们分析一下这两种误差的来源。在采样之后，数据集可以认为被分成了两部分：采样了的数据和未采样的数据。采样误差和噪声误差分别来源于非采样部分和采样部分。在当前的采样机制中，采样阈值 $t$ 控制了每个数据的采样概率，也对这两个误差有着不同的影响。$t$ 越小，则大部分数据都被采样到，这将导致采样误差较小而噪声误差较大。反之亦然。

本质上来说，这两种误差可以认为是两种 privacy budget waste，即隐私预算浪费。首先我们看没有采样到的数据：这些数据进行了完全的隐私保护，也就是说他们的隐私预算根本没有用过到，因此这些用户的隐私预算被浪费掉了。然后对于采样到的数据，阈值 $t$ 被用来控制进行噪声生成，对于隐私预算比 $t$ 高的用户，加参数为 $t$ 的噪声太大了，也使得用户的隐私预算被浪费了。图3展示了两种隐私预算浪费的示例。

Our Utility-aware Sampling Mechanism

Main Idea 为了防止上面提到的两种隐私预算浪费，本文设计了 utility-aware 的采样机制。其采用多轮计算的方式重复利用浪费掉的隐私预算。同时在每轮计算中，本文提供了最优参数的计算方法。Utility-aware 的采样机制可以在不损失隐私保护的前提下提升数据效用。

图4展示了 utility-aware 采样机制的框架。在第 $i$ 轮中，此方法首先决定阈值 $t_i$，然后根据此阈值从真个数据集中进行采样，并根据采样的数据集得到DP的估计结果 $r_i$。此外，utility-aware 采样还计算剩余的个性化隐私预算，并且此隐私预算用于下一轮迭代。本文所提出的机制重复此过程，直到采样的数据集中的数据量小于给定的值。此值用过滤参数 $\alpha \in(0,1)$ 控制。在采样结束后，本文提出的方法通过对所有伦次中的结果 $r_i$ 进行集成，得到最终输出 $r$。然后我们介绍一下此方法的几个关键步骤：

• 阈值计算：此步骤结合最小浪费隐私预算的目标，根据剩下的隐私预算 $S_r$ 计算采样阈值 $t$。给定阈值 $t$，隐私预算浪费可以从采样误差和噪声误差两部分进行计算，即总的浪费可以表示为：

  $$B W\left(t, \mathcal{S}_{r}\right)=\omega_{s} \cdot \sum_{i: \epsilon_{r i}<t} \epsilon_{r i} \times\left(1-\pi_{i}\right)+\omega_{n} \cdot \sum_{i: \epsilon_{r i}>t}\left(\epsilon_{r i}-t\right)$$

  其中，$\epsilon_{ri}$ 表示 $S_r$ 中 $u_i$ 的隐私预算，$\pi_i$ 表示采样概率。$\omega_{s},\omega_{n}$ 分别表示两种隐私预算浪费的权重（$\omega_{s}+\omega_{n}=1$）。因此最优的阈值 $t$ 求解等价于求解一下优化目标：

  $$\begin{align} t &= \min BW(t, S_r),\\ \operatorname{s.t.} &\quad \min S_r \le t \le \max S_r \end{align}$$

• 采样：在计算出阈值之后，对于每一轮的数据，采用 Sampling Mechanism 进行采样，然后计算当前的隐私预算剩余量 $S_r$，并将其用于下一轮计算。

• 差分隐私计算：采样的数据被用来执行差分隐私计算，这当中可以用任何满足差分隐私的机，比如拉普拉斯机制、指数机制等。
• 结果集成：迭代结束之后，我们就获得了一系列估计结果，可表示为：$\mathcal{R}=\left\{r_{1}, r_{2}, \ldots, r_{n}\right\}$。本文提出的 utility-aware 对每个结果进行一定的权重，$r_i$ 的权重 $w_i$ 取决于采样阈值 $t_i$ 和采样数据集 $D_i$ 的大小 $n_i$。

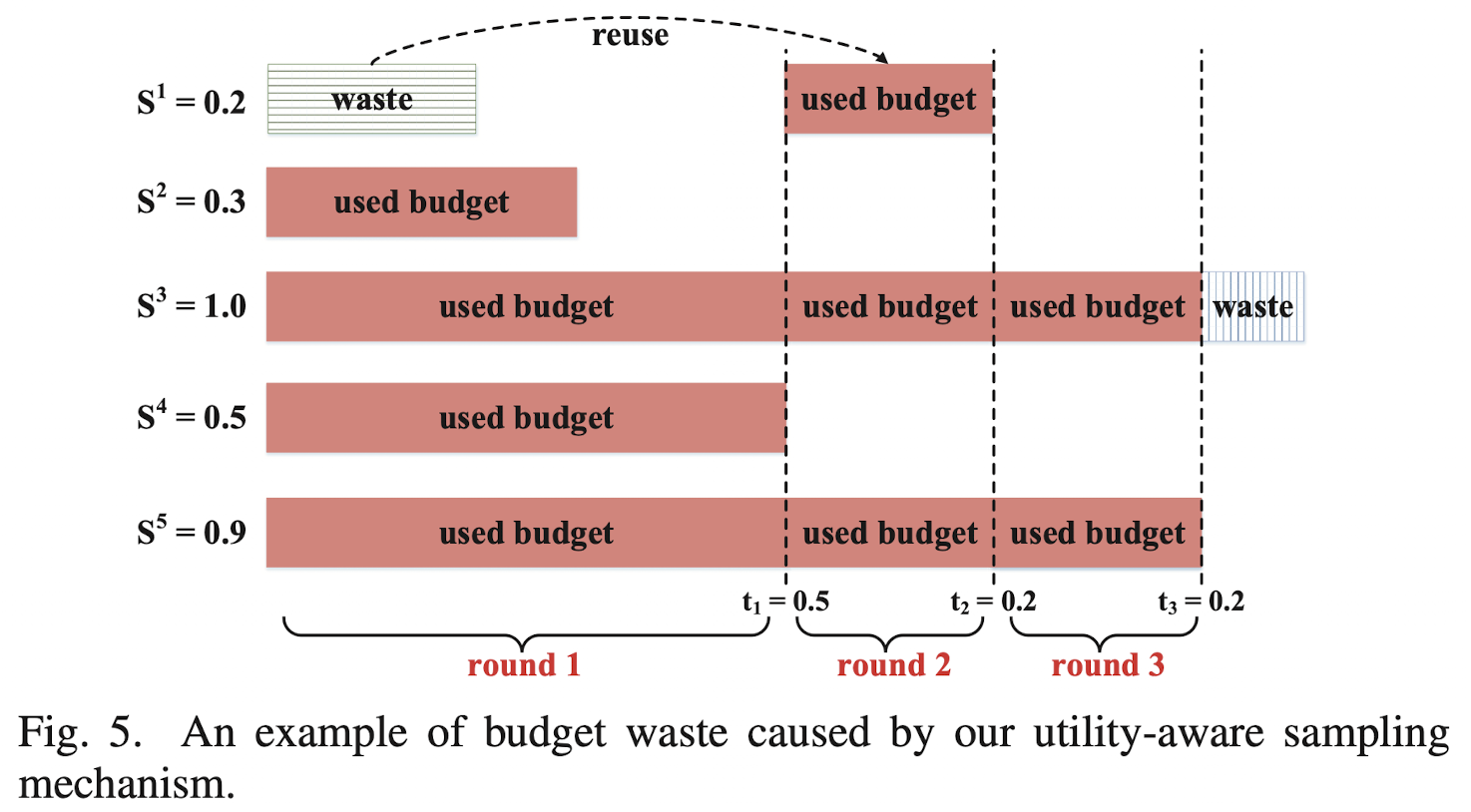
图5展示了本文提出算法可以通过多轮重利用隐私预算的方式降低隐私预算浪费。作为例子，假定 $\mathcal{S}=\langle 0.2,0.3,1.0,0.5,0.9\rangle$，在第一轮中，假定计算的阈值为 $t_{1}=0.5$，然后采样的过程中，采样到了数据（2,3,4,5）。那么剩余的隐私预算为 $\mathcal{S}_{r}=\langle 0.2,0,0.5,0,0.4\rangle$。对于隐私预算低于阈值的，如果当前采样到了，则其所有的隐私预算都用完了。然后在下一轮迭代当中，假如计算的阈值是 $t_2 = 0.2$，那么采样过程会采样到（1,3,5），这时候剩下的隐私预算为：$\mathcal{S}_{r}=\langle 0,0,0.3,0,0.2\rangle$。然后假设下一轮中，阈值依然是$t_3 = 0.2$，这时候剩下的数据就只有第三条了。如果这时候停止了，那么总的隐私预算浪费是0.1。而如果不采用多轮循环的方式，隐私预算浪费是1.1。由此可见，此utility-aware方案可以更好地用好隐私预算。

Privacy Analysis

证明过程：前面说过，我认为此论文的核心假设和证明过程是错误的。因此，证明的过程和我的疑问我将会在后续的讨论章节进行给出。

Algorithm Selection and Calculation

Algorithm Selection

在此步骤中，本框架要选取一个噪声生成算法，用于后续的采样过程。根据不同的查询目标，本文的噪声生成算法来源于：基于 Laplace 的方法，基于指数的方法和 Subsample-and-aggregate 方法。

在某些场合中，直接在数据上加噪可能会导致数据不可用，比如竞拍场景。根据是否能对数据进行加噪，上面三个加噪机制可以被分成以下两类。可以加噪的机制又可被细化为两类：高敏感度的和低敏感度的。本文的机制对于低敏感度采用 Laplace 机制，高敏感度的采用 Subsample-and-aggregate 机制。对于不能直接加噪的，可以采用指数机制保证数据的真实性。

Parameter Calculation

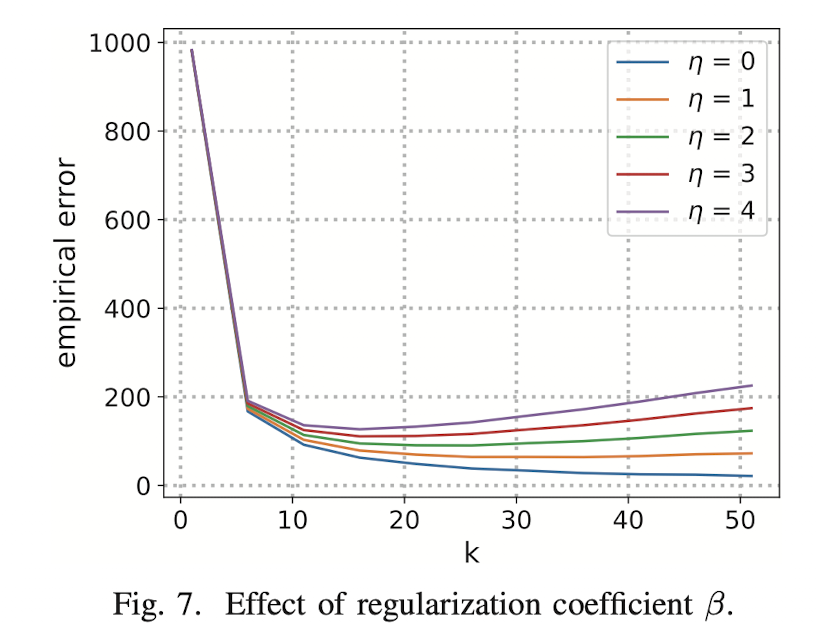
此步骤中，本文提出的框架计算不同不同参数的最优值。AdaPDP中，一共包含四个参数：过滤参数 $\alpha$，采样误差权重 $\omega_{s}$，噪声误差权重 $\omega_{n}$ 和数据块数量 $k$。不像其他三个参数，参数 $k$ 仅仅在Subsample-and-aggregate中进行使用。

然后，本文进行了一些试验来解释参数选取的过程。假设有一个数据集$D^{n p}$，其中的数据都是从分布 $D$ 中独立的。然后参数 $\mathcal{S}$ 是公共参数。在试验阶段，请求函数假设是求中位数，数据集 $D^{n p}$ 中有1000条数据，服从均值为200，方差为50的正态分布。

Calculating $\alpha$

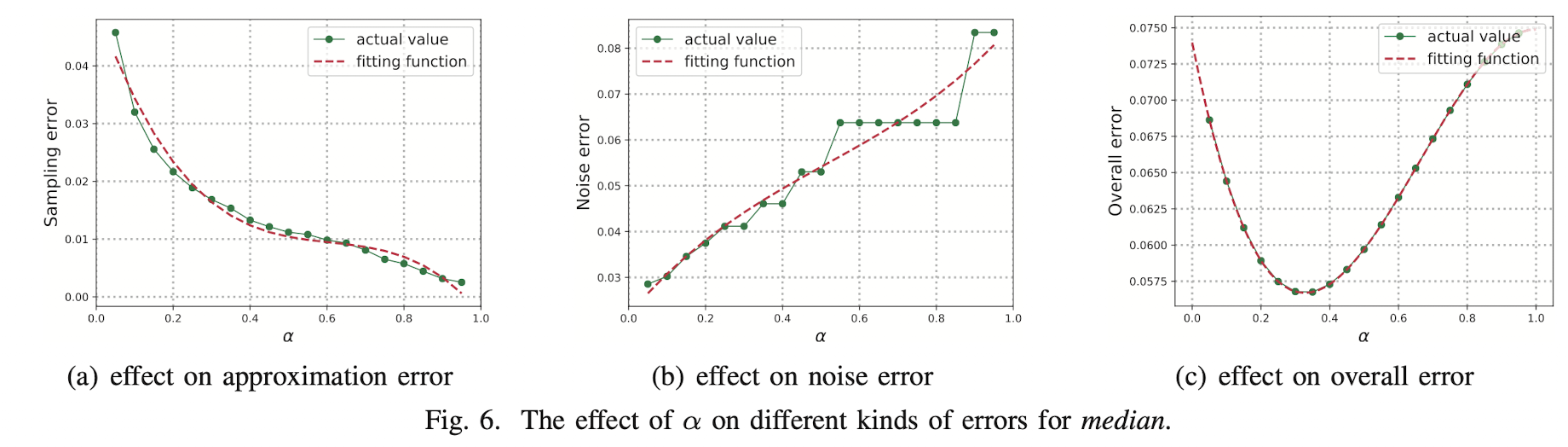
Utility-aware sampling 并不是理论上对所有的最优参数进行求解，而是通过实验的方式根据采样的数据集，给出最优参数。过滤参数 $\alpha$ 的作用是用来过了数据量较小的采样数据集对应的中间估计结果。$\alpha$ 越小，那么有效的采样数据集就越多，但是这些数据集上的查询结果不一定准确。然后，定义4给出了什么样的估计是一个好的估计。

定义4（好估计）：函数 $f:\mathcal{D}\rightarrow \mathcal{R}$ 在输入数据 $x$ 上利用样本 $n’$ 的估计的准确率是 $\gamma$ ，如果 $\Pr[d_{\mathcal{R}}(f(x’),f(x))\le\gamma] \ge \frac{3}{4}$，其中 $x’$ 表示数量为 $n’$ 的采样数据集，$d_{\mathcal{R}}$ 是表示误差。

Sampling Error

讨论

在证明这个东西之前，首先引入一个组合定理。

定理2：令 $\mathcal{M}_{1}: \mathcal{D}_{1} \rightarrow R$ 和 $\mathcal{M}_{2}: \mathcal{D}_{1} \rightarrow R$ 分别表示两个满足 $\mathcal{S}_1$ 和 $\mathcal{S}_2$ 的 PDP 机制。令 $\mathcal{D}_3 = \mathcal{D}_1 \cup\mathcal{D}_2$，那么对于任何 $D\subset \mathcal{D}_3$，机制 $\mathcal{M}_{3}(D)=h\left(\mathcal{M}_{1}\left(D \cap \mathcal{D}_{1}\right), \mathcal{M}_{2}(D \cap D_2)\right)$ 满足 $\mathcal{S}_3$-PDP，其中：$\mathcal{S}_{3}=\left(\left\{\epsilon_{1 a}+\epsilon_{2 a} \mid a \in \mathcal{U}_{1} \cap \mathcal{U}_{2}\right\} \cup \left\{\epsilon_{1 b} \mid b \in \mathcal{U}_{1} \backslash \mathcal{U}_{2}\right\} \cup\left\{\epsilon_{2 c} \mid c \in \mathcal{U}_{2} \backslash \mathcal{U}_{1}\right\}\right)$，$h$ 表示任意输入为 $\mathcal{M}_1, \mathcal{M}_2$ 的函数。

上述定理的理解思路也很简单，也就是说，如果某个数据被哪个机制用了，就提供对应的保护程度，如果两个机制都用了，则保护程度变弱，也就是隐私预算相加。

定理1：本文提出的 Utility-aware 采样机制满足 $\mathcal{S}$-PDP.