标题&地址:Federated Learning With Differential Privacy: Algorithms and Performance Analysis
作者:
发表会议:TIFS’2020

文章总结
联邦学习(FL)作为分布式机器学习的一种方式,能够显著地保护客户端的私有数据不被外部对手揭示。然而,通过分析来自客户端的上传参数的差异(例如深度神经网络中训练的权重),泄露私有信息仍然可能。本文提出了一种基于差分隐私(DP)概念的新框架,其中在聚合之前在客户端的参数中添加噪声,即 noising before model aggregation FL(NbAFL)。首先,我们证明了 NbAFL 可以通过适当调整人工噪声的不同方差来满足不同保护级别的 DP。然后,我们开发了在 NbAFL 中训练的 FL 模型的损失函数的理论收敛界限。具体而言,理论上的收敛界限揭示了以下三个关键特性:1)收敛性能和隐私保护级别之间存在权衡,即更好的收敛性能会导致更低的保护级别;2)在给定的隐私保护级别下,参与 FL 的客户端总数 N 的增加可以提高收敛性能;3)对于给定的收敛性能,存在最大聚合次数(通信轮数)的最优数量。此外,我们提出了一种 K-随机调度策略,在每次聚合中从 $N$ 个客户端中随机选择 $K(1 < K < N)$个客户端参与。我们还开发了在这种情况下损失函数的相应收敛界限,K-随机调度策略也可以保持以上三个特性。此外,我们发现,在固定的隐私级别下,存在最佳的 $K$ 值,可以实现最佳的收敛性能。评估结果表明,我们的理论结果与模拟结果一致,从而有助于设计具有不同收敛性能和隐私保护级别的各种隐私保护 FL 算法。
背景
联邦学习可以认为是这么一个过程,假设 $\mathcal{D}_i$ 是第 $i$ 个用户的本地数据集,那么服务端的总模型为:
其中 $\mathbf{w}_i$ 是第 $i$ 个用户的本地参数,$p_i$ 是权重(比如用数据量占比表示)。在此基础上,联邦学习可以认为是一个优化问题,即希望求得:
其中,$F_i(\cdot)$ 是本地的 loss 函数。

如上图所示,一般来说,联邦模型训练分为以下四步:
- 步骤 1:本地训练(Local training):所有活跃的客户端本地计算训练梯度或参数,并将本地训练的 ML 参数发送到服务器;
- 步骤 2:模型聚合(Model aggregating):服务器对来自 N 个客户端上传的参数进行安全聚合,而不学习本地信息;
- 步骤 3:参数广播(Parameters broadcasting):服务器将聚合参数广播给 N 个客户端;
- 步骤 4:模型更新(Model updating):所有客户端使用聚合参数更新各自的模型,并测试已更新模型的性能。
虽然联邦学习从流程上保护了用户本地的数据不上传到服务器,但是根据上图,用户上传过程的本地模型参数和服务器下发过程的全局模型参数依然有可能被攻击者利用。本文总的来说就是利用差分隐私在一定程度上解决上述两个隐私问题,同时使得模型的收敛性不会因为添加了噪声而受到过多影响,也就是常说的 trade-off。
对于差分隐私,本文采用了高斯机制。todo
论文中用到的符号如下表所示:

FL with DP
在开始分析之前,我们有两个假设:
- 梯度是进行了裁剪(Gradient Clipping)的,即:$\left|\mathbf{w}_i\right| \leq C$
- 每个客户端至少拥有 $m$ 条数据
- 用户本地有 $L$ 个参数(原话为:considering $L$ exposures of local parameters)
首先,客户端本地的权重计算过程为:
(附带一句,这里的 argmin 应该写到求和符号之前。)那么敏感度就可以这么算:
然后,结合每个用户本地的数据量,那么全局的敏感度为:
结合参数量为 $L$,那么 DP 的加噪参数为:$\sigma_{\mathrm{U}}=c L \Delta s_{\mathrm{U}} / \epsilon$。每个梯度上加上这个噪声即可。
对于 Server,其计算的权重参数为:
作者接下来在 Lemma 1 中,证明了这个 $\mathcal{D}_i$ 的敏感度为:$\Delta s_{\mathrm{D}}^{\mathcal{D}_i}=\frac{2 C p_i}{m}$。因此,其敏感度为:
经过上面的分析,也就是说整个训练过程中有两处加噪:1)客户端对本地梯度加噪(上传通道);2)Server 对求和结果加噪(下载通道)。所以,总的算法:Noising before Aggregation FL 的流程如算法 1 所示:

这里需要继续考虑一个问题,上面分析了下载通道中的敏感度,虽然高斯机制有了敏感度之后就可以计算方差,但是作者给了一个定理 1,说在 $T$ 次的汇聚当中,给定 $L,N$,下载通道的 DP 参数为:
也就是说,服务端是否添加噪声由:聚合次数 $T$,参数量 $L$ 和客户端数量 $N$ 三个参数共同决定。从上面的公式直接来看,$T$ 越大,那么信息泄露的可能性越大,所以噪声要添加。而 $N$ 越大,则客户端数量越大,单个客户端泄露的可能性就越低。但是这里我一直没太明白 $L$ 的作用,根据上式,$L$ 越大,就约不需要添加噪声了。
有了上面的算法之后,作者单独写了一章证明 NbAFL 算法的收敛性,这部分我就没有深入了解了。
K-Client Random Scheduling Policy
前面介绍了 $N$ 个所有客户端共同参与联邦学习的 NbAFL 算法。在此基础上,作者提出了一个 K-Client 的调度策略。有意思的结论是作者表明:从 $N$ 个客户端中选择 $K$ 个参与训练,实验证明收敛性能更好。
客户端本地加噪的过程和所有客户端都参与的情况一样。不同的是,在 $K$ 个客户端参与的情况下,下载通道的加噪有点区别。其参数这样设置:
其中的参数值为:$b=-\frac{T}{\epsilon} \ln \left(1-\frac{N}{K}+\frac{N}{K} e^{\frac{-\epsilon}{T}}\right), \gamma=-\ln \left(1-\frac{K}{N}+\frac{K}{N} e^{\frac{-\epsilon}{L \sqrt{K}}}\right)$。
然后作者在 Remark 5 中表明:存在一个最优的 $K\in[0, N]$ 达到最好的收敛性,使得 K-Client 策略优于所有客户端的情况。
实验
作者使用的实验设置比较简单,不翻译了直接贴过来:We conduct experiments on the standard MNIST dataset for handwritten digit recognition consisting of 60000 training examples and 10000 testing examples [34]. Each example is a 28 × 28 size gray-level image. Our baseline model uses a a MLP network with a single hidden layer containing 256 hidden units. In this feed-forward neural network, we use a ReLU units and softmax of 10 classes (corresponding to the 10 digits) with the cross-entropy loss function. For the optimizer of networks, we set the learning rate to 0.002.
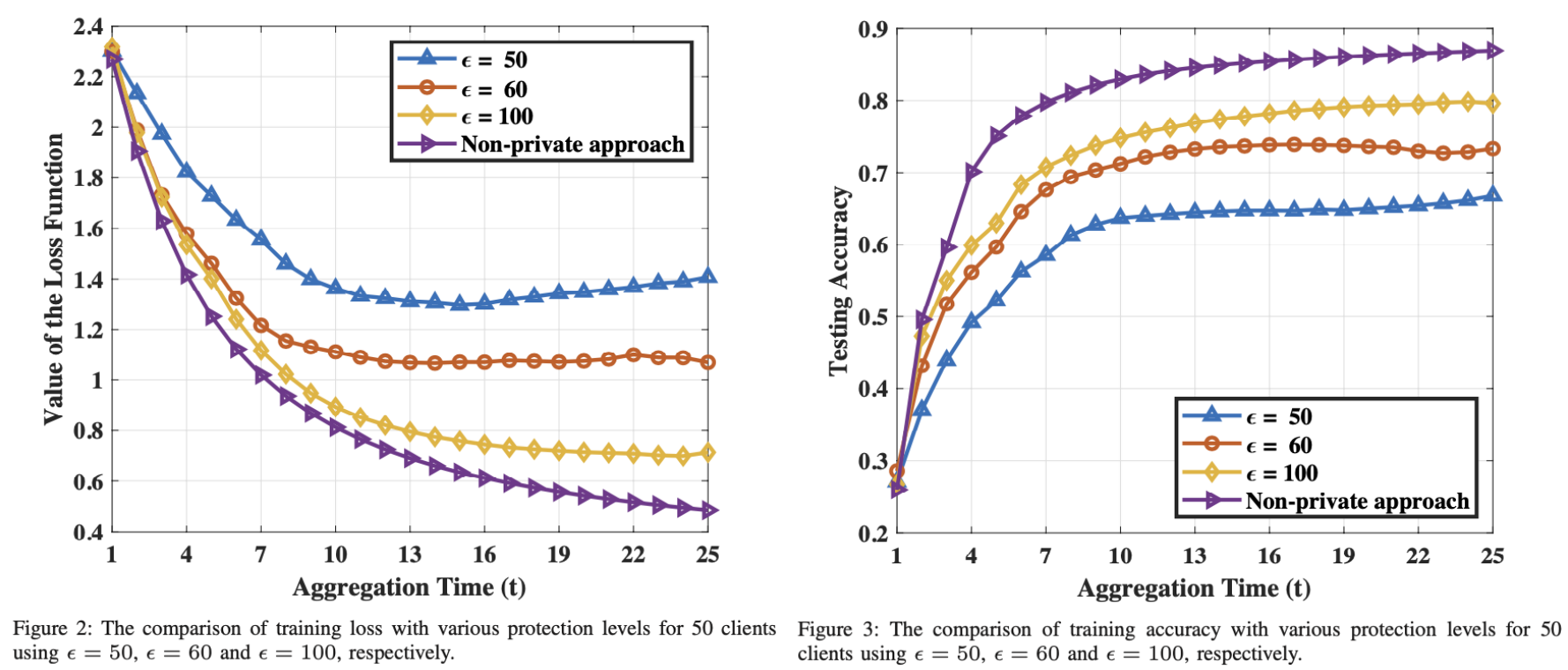
图 2 和图 3 展现了不同 epsilon 下的 loss,此实验中参数为:$N=50,T=25,\delta=0.01$。这个实验效果也没啥好分析的。

图 4 和图 5,展示了 $N=50,K=20$ 下的 K-Client 策略,对比没有图 2 和 3,可以看出收敛速度确实是更快的。
然后图 6 和图 7 固定 $\epsilon=60,\delta=0.01$,展示了不同参与者数量(参考 Remark.3)下的收敛速度。参与者越多,数据量也就越大,因此收敛更快。

图 8 和图 9 展示了聚合次数 $T$ 的影响,图 8 展示了理论上界随着 T 的变化情况。图 9 展示了理论和实验结果。此结果和 Remark 4 结论相符合,这部分理论在收敛性分析当中。
图 11 设定 $N=50$ 下,探求不同客户端数量对收敛的影响,可以验证 K-Client 策略的准确性。
本篇内容到这里就结束了,欢迎关注公众号《差分隐私》,获取更多前沿技术。